Bài tập 3 trang 51 SGK Hình học 12
Bài tập 3 trang 51 SGK Hình học 12
Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với (ABC) và có SA = a, AB = b và AC = c. Mặt cầu đi qua các đỉnh A,B,C,S có bán kính r bằng
(A) \(\frac{2(a+b+c)}{3}\) (B) \(2\sqrt{a^2+b^2+c^2}\)
(C) \(\frac{1}{2}\sqrt{a^2+b^2+c^2}\) (D) \(\sqrt{a^2+b^2+c^2}\)
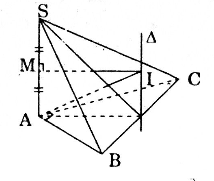
Gọi O là trung điểm của BC ⇒ O là tâm đường tròn ngoại tiếp tam giác ABC. Đường thẳng \(\Delta\) là trục của đường tròn tâm O.
Gọi I là giao điểm của mặt phẳng trung trực của SA và \(\Delta\). Khi đó I là tâm của mặt cầu đi qua A, B, C, S và r = IA.
Bán kính mặt cầu này là
\(r=IA=\sqrt{OA^2+IO^2} =\sqrt{\left (\frac{BC}{2} \right )^2+\left (\frac{SA}{2} \right )^2}\)
\(= \frac{1}{2}\sqrt{a^2+b^2+c^2}\)
⇒ Chọn đáp án C
-- Mod Toán 12
Copyright © 2021 HOCTAP247
