Trang chủ
Lớp 12
Toán Lớp 12 SGK Cũ
Chương 2: Mặt Nón, Mặt Trụ, Mặt Cầu
Bài tập 1 trang 51 SGK Hình học 12
Bài tập 1 trang 51 SGK Hình học 12
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 1 trang 51 SGK Hình học 12
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A'B'C'D'. Diện tích S là.
(A) \(\pi a^2\)
(B) \(\pi a^2\sqrt{2}\)
(C) \(\pi a^2\sqrt{3}\)
(D) \(\frac{\pi a^2\sqrt{2}}{2}\)
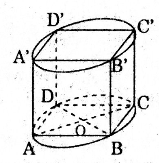
Bán kính đường tròn ngoại tiếp hình vuông ABCD là \(r=OA=\frac{1}{2} AC=\frac{a\sqrt{2}}{2}\)
Diện tích xung quanh của hình trụ là: \(S_{xq} =2 \pi r. \l=2\pi .\frac{a\sqrt{2}}{2}.a=\pi a^2\sqrt{2}\)
⇒ Chọn đáp án B
-- Mod Toán 12
Copyright © 2021 HOCTAP247
