Bài tập 5 trang 50 SGK Hình học 12

Bài tập 5 trang 50 SGK Hình học 12

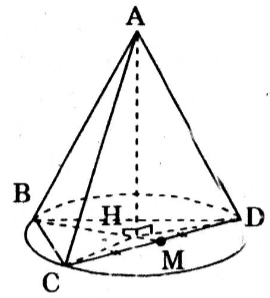
Câu a:
Xét 3 tam giác AHB, AHC, AHD có: chung cạnh AH và AB = AC = AD = a

\(\Rightarrow \Delta AHB=\Delta AHC=\Delta AHD\)

\(\Rightarrow HB= HC= HD\) hay H là tâm đường tròn ngoại tiếp \(\Delta BCD.\)

Do \(\Delta BCD.\) là tam giác đều BM là trung trực của \(\Delta BCD.\) nên BM cũng là trung tuyến.

\(\Rightarrow BM=\frac{a\sqrt{3}}{2}\Rightarrow BH=\frac{2}{3}BM=\frac{a\sqrt{3}}{3}\)

Xét tam giác vuông ABH, ta có:

\(AH=\sqrt{AB^2-BH^2}=\frac{a\sqrt{6}}{3}\)

Câu b:

Hình trụ có đường tròn đáy ngoại tiếp \(\Delta BCD\) và chiều cao AH thì bán kính hình trụ là:

\(r=BH=\frac{a\sqrt{3}}{3}\Rightarrow S_{xq}=2\pi.r.AH=2 \pi.\frac{a\sqrt{6}}{3}.\frac{a\sqrt{3}}{3} =\frac{2\pi a^2\sqrt{2}}{3}\)

Thể tích của khối trụ là:
\(V=\pi.r^2.AH= \pi \left ( \frac{a\sqrt{3}}{3} \right )^2.\frac{a\sqrt{6}}{3}=\frac{\pi a^3\sqrt{6}}{9}\)

-- Mod Toán 12