Bài tập 2 trang 63 SGK Hình học 12 NC

Bài tập 2 trang 63 SGK Hình học 12 NC

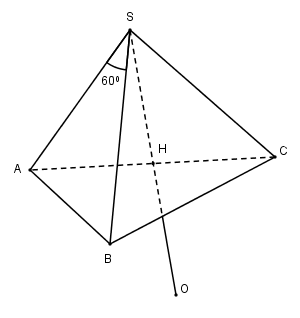
Áp dụng định lí Cosin trong tam giác SAB, SAC ta có:

\(\begin{array}{l}
A{B^2} = S{A^2} + S{B^2} - 2SA.SB.\cos {60^0}\\
 = {a^2} + {a^2} - 2{a^2}.\frac{1}{2} = {a^2} \Rightarrow AB = a\\
A{C^2} = S{A^2} + S{C^2} - 2SA.SC.\cos {120^0}\\
 = {a^2} + {a^2} - 2{a^2}\left( { - \frac{1}{2}} \right) = 3{a^2} \Rightarrow AC = a\sqrt 3 
\end{array}\)

Trong tam giác vuông SBC có 

\(B{C^2} = S{B^2} + S{C^2} = 2{a^2} \Rightarrow BC = a\sqrt 2 \)

Ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại B

Gọi H là trung điểm của AC thì H là tâm đường tròn ngoại tiếp tam giác ABC.

Vì SA = SB = SC nên SH ⊥ mp(ABC) và

\(\begin{array}{l}
S{H^2} = S{C^2} - H{C^2}\\
 = {a^2} - {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{{a^2}}}{4} \Rightarrow SH = \frac{a}{2}
\end{array}\)

Gọi O là điểm đối xứng của S qua H thì SO = OA = OB = OC = a nên mặt cầu ngoại tiếp hình chóp S.ABC có tâm O và bán kính R = a.

-- Mod Toán 12