Bài tập 3 trang 61 SGK Giải tích 12

Bài tập 3 trang 61 SGK Giải tích 12

Nhận xét:

Bài tập này chủ yếu để các em ghi nhớ các tính chất của hàm số lũy thừa, để giải ta vận dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số đã học ở chương I.

Lời giải:

Ta có lời giải chi tiết các câu a, b bài 1 như sau:

Câu a:

Xét hàm số \(y=x^\frac{4}{3}\)

Tập xác định: D=(0;+∞).

Sự biến thiên:\(y' = \frac{4}{3}{x^{\frac{1}{3}}} > 0,\forall x > 0\) nên hàm số luôn luôn đồng biến trên (0;+∞).

Giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to {0^ + }} y = 0;\mathop {\lim }\limits_{x \to + \infty } y = + \infty\) nên đồ thị hàm số không có tiệm cận.

Bảng biến thiên: 

Đồ thị của hàm số:

Đồ thị hàm số đi qua điểm (1;1) và \(\left ( 2;2^\frac{4}{3} \right )\).

Câu b:

Xét hàm số \(\small y=x^{-3}\)

Tập xác định: \(D = \mathbb{R}\backslash {\rm{\{ 0\} }}{\rm{.}}\)

Sự biến thiên: \(y' = - 3{x^{ - 4}} = - \frac{3}{{{x^4}}} < 0,\forall x \ne 0.\)

Giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to \pm \infty } y = 0\) nên đồ thị hàm số nhận đường thẳng y=0 làm tiệm cận ngang và nhận đường thẳng x=0 là tiệm cận đứng. 

Vậy hàm nghịch biến trong hai khoảng (-∞;0) và (0; +∞).

Bảng biến thiên:

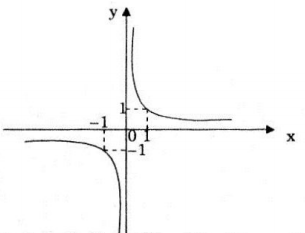
Đồ thị hàm số:

Đồ thị hàm số nhận điểm (0;0) làm tâm đối xứng.

Đồ thị hàm số đi qua các điểm (1;1) và (-1;-1).

Đồ thị hàm số:

-- Mod Toán 12