Bài tập 8 trang 90 SGK Giải tích 12

Bài tập 8 trang 90 SGK Giải tích 12

Vậy dụng các phương pháp giải bất phương trình mũ và lôgarit  đã học ở bài 6 chương 2 Giải tích 12 ta có lời giải chi tiết câu a, b, c, d bài 8 như sau:

Câu a:

2^2x-1+ 2x^2x-2 + 2^2x-3 ≥ 448

Ta có:

⇔ 2².2^2x-3 + 2.2^2x-3 +2^2x-3 ≥ 448

⇔7.2^2x-3 ≥ 448 ⇔2^2x-3 ≥ 64  ⇔ 2x – 3 ≥ 6

⇔ x ≥ \(\frac{9}{2}\)

Câu b:

0,4^x - 2,5^x+1 > 1,5

\(\Leftrightarrow \left ( \frac{2}{5} \right )^x-\left ( \frac{5}{2} \right )^{x+1}>\frac{3}{2} \Leftrightarrow \left ( \frac{2}{5} \right )^x-\frac{5}{2}.\left ( \frac{5}{2} \right )^x>\frac{3}{2}\)

Đặt \(\left ( \frac{2}{5} \right )^x=t\Rightarrow \left ( \frac{5}{2} \right )^x=\frac{1}{t}\)

Bất phương trình trở thành

\(t-\frac{5}{2}.\frac{1}{t}> \frac{3}{2}\Leftrightarrow t-\frac{5}{2t}>\frac{3}{2} \Leftrightarrow \frac{2t^2-3t-5}{2t}>0\)

\(\Leftrightarrow \frac{(2t-5)(t+1)}{2t}>0 \ (2)\)

Bảng xét dấu

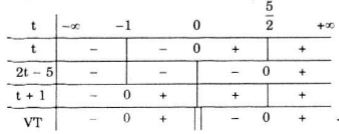
⇒ (2) có nghiệm -1 < t < 0 hoặc \(t> \frac{5}{2}\)

Với -1 < t < 0 thì \(-1 <\left ( \frac{2}{5} \right )^x<0\) (vô nghiệm)

Với \(t> \frac{5}{2}\) thì \(( \frac{2}{5})^x>\frac{5}{2}\Leftrightarrow \left ( \frac{2}{5} \right )^x> \left ( \frac{2}{5} \right )^{-1} \Leftrightarrow x<-1\)

Câu c:

\(log_3\left [ log_\frac{1}{2}(x^2-1) \right ]<1\) (3)

ĐK: \(-\sqrt{2}<x<-1\) hoặc \(1<x<\sqrt{x}\)

Khi đó: \((3)\Leftrightarrow log_{\frac{1}{2}}(x^2-1)<3\Leftrightarrow x^2-1> \frac{1}{8}\Leftrightarrow x^2> \frac{9}{8}\)

\(\Leftrightarrow \Bigg \lbrack \begin{matrix} x>\frac{3}{2\sqrt{2}}\\ \\ x< -\frac{3}{2\sqrt{2}} \end{matrix}\)

Kết hợp với điều kiện ta được nghiệm của bất phương trình là:

\(-\sqrt{2}<x< \frac{-3}{2\sqrt{2}}\) hoặc \(\frac{3}{2\sqrt{2}}<x<\sqrt{2}\).

Câu d:

\(log_{0,2}^2x-5log_{0,2}x < -6\)

ĐK: x >  0

Đặt log_0,2 x = t.

Phương trình trở thành \(t^2-5t+6<0\Leftrightarrow 2<t<3\)

Với \(2<t<3\) thì \(2<log_{0,2}x < 3\Leftrightarrow 0,2^3 <x <0,2^2 \Leftrightarrow \frac{1}{125}< x< \frac{1}{25}\)

Kết hợp với điều kiện ta được nghiệm của bất phương trình trình là:

\(\frac{1}{125}< x< \frac{1}{25}\).

-- Mod Toán 12