Bài tập 33 trang 126 SGK Toán 10 NC
Bài tập 33 trang 126 SGK Toán 10 NC
Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:
a) \(-x^2+x+6\)
b) \(2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
a) Đặt \(f(x)=-x^2+x+6\)
Ta có \( f(x)=- {x^2} + x + 6 = - \left( {x + 2} \right)\left( {x - 3} \right) = \left( { - x - 2} \right)\left( {x - 3} \right)\)
Bảng xét dấu
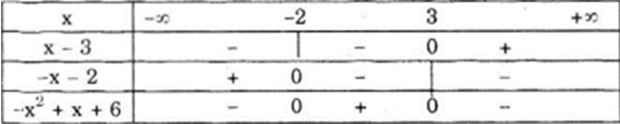
Vậy \(f\left( x \right) < 0\) với \(\left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) > 0\) với (- 2;3)
\(f(x)=0\) tại x = - 2 và x = 3
b) Đặt \(f(x)=2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
Ta có \(f(x) = 2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 = 2\left( {x - 1} \right)\left( {x - \frac{{\sqrt 3 }}{2}} \right) = \left( {x - 1} \right)\left( {2x - \sqrt 3 } \right)\)
Bảng xét dấu
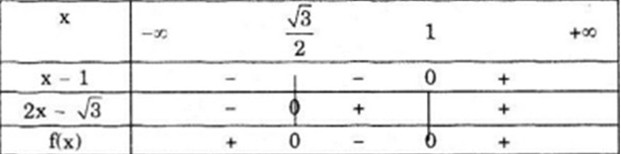
Vậy \(f\left( x \right) < 0\) với \({\left( {\frac{{\sqrt 3 }}{2};1} \right)}\)
\(f\left( x \right) > 0\) với \(\left( { - \infty ;\frac{{\sqrt 3 }}{2}} \right) \cup \left( {1; + \infty } \right)\)
\(f(x)=0\) tại \(x={\frac{{\sqrt 3 }}{2}}\) và x = 1
-- Mod Toán 10
Copyright © 2021 HOCTAP247
