Bài tập 43 trang 132 SGK Toán 10 NC

Bài tập 43 trang 132 SGK Toán 10 NC

a) Ta có

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{\frac{x}{2} + \frac{y}{3} - 1 > 0}\\
{2\left( {x - 1} \right) + \frac{y}{2} < 4}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3x + 2y - 6 > 0}\\
{4x + y - 12 < 0}
\end{array}} \right.
\end{array}\)

Miền nghiệm của hệ là miền không bị gạch chéo (không kể biên) như hình vẽ:

b) Ta có

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{4x - 5y + 20 > 0}\\
{y > 0}\\
{ - y + 5 > \frac{{x - 3}}{3}}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{4x - 5y + 20 > 0}\\
{y > 0}\\
{x + 3y - 18 < 0}
\end{array}} \right.
\end{array}\)

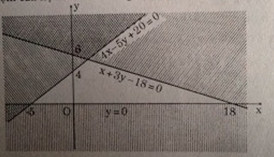
Miền nghiệm của hệ là miền không bị gạch (không kể biên) trên hình.

-- Mod Toán 10