Bài tập 2 trang 99 SGK Đại số 10

Bài tập 2 trang 99 SGK Đại số 10

Câu a:

Ta có: \(\left\{ {\begin{array}{*{20}{c}}
{x - 2y < 0}\\
{x + 3y >  - 2}\\
{y - x < 3}
\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}
x - 2y < 0\\
x + 3y >  - 2\\
y - x < 3
\end{array} \right.\)

Gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là ba đường thẳng có phương trình là:

\(x - 2y = 0;x + 3y + 2 = 0;\)

x - y + 3 = 0

Lấy điểm M(1;0), ta có:

1 - 2.0 = 1 > 0

1 + 3.0 + 2 = 3 >0;

1 - 0 + 3 = 4 > 0

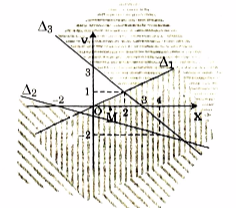
Vẽ \({\Delta _1},{\Delta _2},{\Delta _3}\) trên hệ trục, ta có:

Vậy tập nghiệm của hệ là miền không gạch

Câu b:

\(\left\{ \begin{array}{l}
\frac{x}{3} + \frac{y}{2} - 1 < 0\\
x + \frac{1}{2} - \frac{{3y}}{2} \le 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2x + 3y - 6 < 0\\
2x - 3y - 3 \le 0\\
x \ge 0
\end{array} \right.\)

Gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là ba đường thẳng có phương trình lần lượt là 2x + 3y - 6 =0;

2x - 3y - 3 = 0; x = 0.

Lấy điểm M(1;1), ta có:

2.1 + 3.1 - 6= -1< 0

2.1 - 3.1 - 3 =-4 < 0; 1 >0

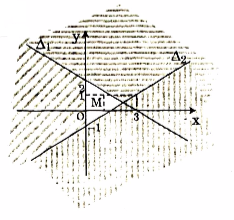
Vẽ \({\Delta _1},{\Delta _2},{\Delta _3}\) trên hệ trục ta có:

⇒ Trên nghiệm của hệ là miền trong của tam giác \({M _1},{M _2},{M _3}\) và hai đoạn thẳng M₁M₂, M₂M₃. Với M₁ là giao của {\Delta _1} và {\Delta _3}, M₂ là giao {\Delta _2},{\Delta _3}M₃ là giao của {\Delta _1} và {\Delta _2}.

-- Mod Toán 10

Video hướng dẫn giải bài 2 SGK