Bài tập 46 trang 135 SGK Toán 10 NC

Bài tập 46 trang 135 SGK Toán 10 NC

a) Ta có \(\left\{ \begin{array}{l}
x - y > 0\\
x - 3y \le  - 3\\
x + y > 5
\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}
x - y > 0\\
x - 3y + 3 \le 0\\
x + y - 5 > 0
\end{array} \right.\)

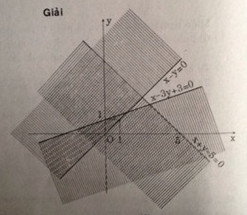
Miền nghiệm là phần mặt phẳng không bị gạch chéo trong đó kể cả những điểm thuộc (d₂) và không kể các điểm trên (d₁ )và (d₃)

Trong đó, (d₁): x - y = 0

(d₂): x - 3y + 3 = 0

(d₃): x + y - 5 = 0

b) Ta có 

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{3x - 2y - 6 \ge 0}\\
{2\left( {x - 1} \right) + \frac{{3y}}{2} \le 4}\\
{x \ge 0}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3x - 2y - 6 \ge 0}\\
{4x + 3y - 12 \le 0}\\
{x \ge 0}
\end{array}} \right.
\end{array}\)

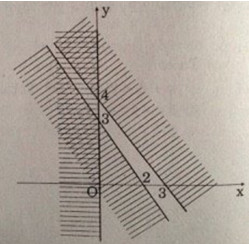
Miền nghiệm là phần mặt phẳng không bị gạch chéo trong đó kể cả những điểm thuộc 3 đường thẳng (d₁), (d₂), (d₃).

Trong đó (d₁): 3x - 2y - 6 = 0

(d₂): 4x + 3y - 12 = 0

(d₃): x = 0

-- Mod Toán 10