Bài tập 82 trang 155 SGK Toán 10 NC

Bài tập 82 trang 155 SGK Toán 10 NC

a) Bảng xét dấu

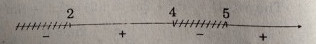
Vậy \(S = \left( {2;4} \right) \cup \left( {5; + \infty } \right)\)

b) Bất phương trình đã cho tương đương với bất phương trình:

\(\begin{array}{l}
\frac{{2{x^2} - 10x + 14}}{{{x^2} - 3x + 2}} - 1 \ge 0\,\,\,\\
 \Leftrightarrow \frac{{2{x^2} - 7x + 12}}{{{x^2} - 3x + 2}} \ge 0
\end{array}\)

Bảng xét dấu

Tập nghiệm của bất phương trình là \(S = \left( { - \infty ;1} \right) \cup \left( {2;3} \right] \cup \left( {4; + \infty } \right)\)

-- Mod Toán 10