Bài tập 1 trang 94 SGK Đại số 10

Bài tập 1 trang 94 SGK Đại số 10

Câu a:

\(2x - 1 = 0 \Leftrightarrow x = \frac{1}{2};x + 3 = 0 \Leftrightarrow x =  - 3\)

Xét dấu f(x) trên tập xác định D = R, ta có"

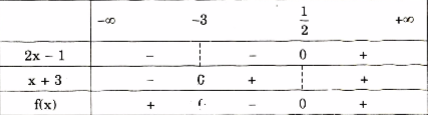
Nhìn vào bảng xét dấu, ta có:

f(x) > 0 khi \(x \in ( - \infty ; - 3) \cup (\frac{1}{2}; + \infty )\)

f(x) < 0 khi \(x \in ( - 3;\frac{1}{2})\) 

f(x) = 0 khi \(x =  - 3;x = \frac{1}{2}\) 

Câu b:

\(- 3x - 3 = 0 \Leftrightarrow x =  - 1;x + 2 = 0 \Leftrightarrow x =  - 2;x + 3 = 0 \Leftrightarrow x =  - 3\)

Bảng xét dấu

Nhìn vào bảng xét dấu, ta có:

f(x) > 0 khi \(x \in ( - \infty ; - 3) \cup ( - 2; - 1)\) 

f(x) < 0 khi \(x \in ( - 3; - 2) \cup ( - 1; + \infty )\) 

f(x) = 0 khi \(x =  - 3;x =  - 2;x =  - 1\) 

Câu c:

\(f(x) = \frac{{ - 4(2 - x) - 3(3x + 1)}}{{(3x + 1)(2 - x)}} = \frac{{ - 5x - 11}}{{(3x + 1)(2 - x)}}\)

Ta có: f(x) không xác định khi \(x = \frac{{ - 1}}{3};x = 2.\)

Các nhị thức \( - 5x - 11;3x + 1;2 - x\) có nghiệm lần lượt là: \(\frac{{ - 11}}{5};\frac{{ - 1}}{3};2.\)

Bảng xét dấu

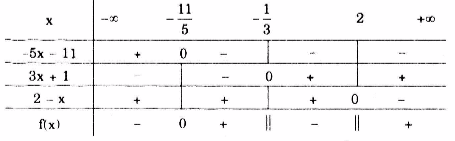
Nhìn vào bảng xét dấu, ta có:

f(x) > 0 khi \(x \in \left( {\frac{{ - 11}}{5};\frac{{ - 1}}{3}} \right) \cup (2; + \infty )\)

f(x) < 0 khi \(x \in \left( { - \infty ;\frac{{ - 11}}{5}} \right) \cup \left( {\frac{{ - 1}}{3};2} \right)\)

f(x) = 0 khi \(x = \frac{{ - 11}}{5}\)  

Câu d:

\(f(x) = 4{x^2} - 1 = (2x - 1)(2x + 1)\)

Các nhị thức: 2x - 1; 2x + 1 có các nghiệm lần lượt là \(\frac{1}{2}; - \frac{1}{2}\)

Bảng xét dấu

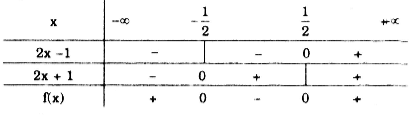
Nhìn vào bảng, ta có:

f(x) > 0 khi \(x \in \left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\)

f(x) < 0 khi \(x \in \left( { - \frac{1}{2};\frac{1}{2}} \right)\)

f(x) = 0 khi \(x =  \pm \frac{1}{2}\)

-- Mod Toán 10

Video hướng dẫn giải bài 1 SGK