Bài tập 53 trang 145 SGK Toán 10 NC

Bài tập 53 trang 145 SGK Toán 10 NC

a) Ta có \( - 5{x^2} + 4x + 12 = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}
x =  - \frac{6}{5}\\
x = 2
\end{array} \right.\)

Bảng xét dấu

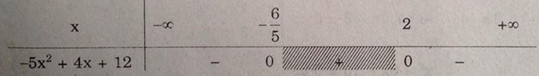 Vậy tập nghiệm là \(S = \left( { - \infty ; - \frac{6}{5}} \right) \cup \left( {2; + \infty } \right)\)

b) Ta có \(16{x^2} + 40x + 25 = 0 \)

\(\Leftrightarrow x =  - \frac{5}{4}\)

\(\begin{array}{l}
a = 16 > 0\\
\Delta ' = 200 - 16.25=-200 < 0\\
 \Rightarrow 16{x^2} + 40x + 25 \ge 0,\forall x \in R
\end{array}\)

Vậy S = Ø

c) Ta có:

a = 3

Δ’ = 4 – 12 = - 8 < 0

⇒ 3x² - 4x + 4 ≥ 0, ∀x ∈ R

Vậy S = R

d) Ta có: \({x^2} - x - 6 = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}
x = 3\\
x =  - 2
\end{array} \right.\)

Bảng xét dấu

Vậy tập nghiệm của bất phương trình là S = [- 2;3]

-- Mod Toán 10