Bài tập 49 trang 140 SGK Toán 10 NC

Bài tập 49 trang 140 SGK Toán 10 NC

a) Ta có:

a = 3 > 0

Δ’ = 1 – 3 = - 2 < 0

⇒ 3x² – 2x + 1 > 0, ∀x  ∈ R

b) Đặt f(x) = - x² + 4x – 1

Ta có:

a = -1 < 0

Δ’ = 4 – 1 = 3 > 0

Tam thức - x² + 4x – 1 có hai nghiệm phân biệt \(x = 2 \pm \sqrt 3 \)

Bảng xét dấu

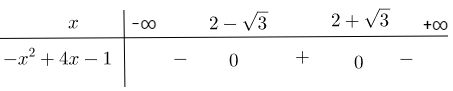
Vậy f(x) > 0 với mọi \(x \in \left( {2 - \sqrt 3 ;2 + \sqrt 3 } \right)\)

f(x) < 0 với mọi \(x \in \left( { - \infty ;2 - \sqrt 3 } \right) \cup \left( {2 + \sqrt 3 ; + \infty } \right)\)

c) Ta có:

a = 1 > 0

Δ = 3 – 3 = 0

\({x^2} - \sqrt 3 x + \frac{3}{4}\) có nghiệm kép là \(x = \frac{{\sqrt 3 }}{2}\)

Suy ra \({x^2} - \sqrt 3 x + \frac{3}{4} > 0,\forall x \ne \frac{{\sqrt 3 }}{2}\)

d) Đặt f(x) = \(\left( {1 - \sqrt 2 } \right){x^2} - 2x + 1 + \sqrt 2 \)

\(\begin{array}{*{20}{l}}
{a = 1 - \sqrt 2  < 0}\\
\begin{array}{l}
\left( {1 - \sqrt 2 } \right){x^2} - 2x + 1 + \sqrt 2  = 0\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{x =  - 3 - 2\sqrt 2 }
\end{array}} \right.
\end{array}
\end{array}\)

Bảng xét dấu

Vậy f(x) > 0 với mọi \(x \in \left( { - 3 - 2\sqrt 3 ;1} \right)\)

f(x) < 0 với mọi \(\left( { - \infty ; - 3 - 2\sqrt 3 } \right) \cup \left( {1; + \infty } \right)\)

-- Mod Toán 10