Bài tập 3 trang 105 SGK Đại số 10

Bài tập 3 trang 105 SGK Đại số 10

Câu a:

Xét tam thức \(f\left( x \right){\rm{ }} = 4{x^2} - x + 1\) có: \(\Delta  = {1^2} - 16 =  - 15 < 0\)

Mà \(a{\rm{ }} = {\rm{ }}4{\rm{ }} > {\rm{ }}0 \Rightarrow f(x) > 0\) với mọi x.

Suy ra bất phương trình vô nghiệm

Câu b:

Xét \(f(x) =  - 3{x^2} + x + 4\) có \(a = b + c =  - 3 - 1 + 4 = 0\)

\( \Rightarrow f(x)\) có 2 nghiệm: \(x =  - 1,x = \frac{4}{3}\)

Mà a = -3 < 0, do đó: \(f(x) \ge 0 \Leftrightarrow  - 1 \le x \le \frac{4}{3}\)

Vậy bất phương trình có nghiệm \( - 1 \le x \le \frac{4}{3}\)

Câu c:

\(\frac{1}{{{x^2} - 4}} < \frac{3}{{3{x^2} + x - 4}}\)

\( \Leftrightarrow \frac{{3{x^2} + x - 4 - 3({x^2} - 4)}}{{({x^2} - 4)(3{x^2} + x - 4)}} < 0 \Leftrightarrow \frac{{x + 8}}{{({x^2} - 4)(3{x^2} + x - 4)}} < 0\)

Lập bảng xét dấu: \(f(x) = \frac{{x + 8}}{{({x^2} - 4)(3{x^2} + x - 4)}},\) ta có

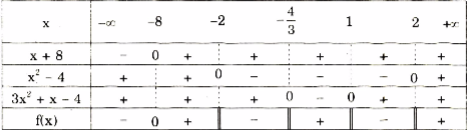
Nhìn vào bảng xét dấu ta có bất phương trình đã cho có nghiệm

\(x \in \left( { - \infty ; - 8} \right) \cup ( - 2; - \frac{4}{3}) \cup (1;2)\)  

Câu d:

Xét \(f(x) = {x^2} - x - 6\) có hai nghiệm x = 3, x = -2, mà hệ số a = 1

Suy ra: \(f(x) \le 0 \Leftrightarrow  - 2 \le x \le 3\)

Vậy bất phương trình có nghiệm: \( - 2 \le x \le 3\)  

-- Mod Toán 10

Video hướng dẫn giải bài 3 SGK