Bài tập 47 trang 135 SGK Toán 10 NC
Bài tập 47 trang 135 SGK Toán 10 NC
Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:
\(\left\{ \begin{array}{l}
2x - y \ge 2\\
x - 2y \le 2\\
x + y \le 5\\
x \ge 0
\end{array} \right.\)
a) Hãy xác định (S) để thấy rằng đó là một tam giác.
b) Trong (S) hãy tìm điểm có tọa độ (x;y) làm cho biểu thức f(x;y) = y − x có giá trị nhỏ nhất, biết rằng f(x;y) có giá trị nhỏ nhất tại một trong các đỉnh của (S).
a) Lần lượt dựng các đường thẳng:
\( - 2x + y = - 2;x - 2y = 2,x + y = 5\) và x = 0
Và dựa vào đó để tìm nghiệm S của hệ bất phương trình
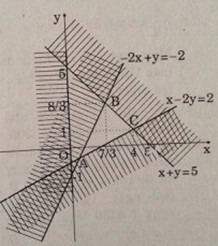
Tập nghiệm S được biểu diễn bằng miền trong của tam giác ABC với:
\(A\left( {\frac{2}{3}; - \frac{2}{3}} \right);B\left( {\frac{7}{3};\frac{8}{3}} \right);C\left( {4;1} \right)\)
b) Tại \(A\left( {\frac{2}{3}; - \frac{2}{3}} \right) \Rightarrow F = - \frac{4}{3}\)
Tại \(B\left( {\frac{7}{3};\frac{8}{3}} \right) \Rightarrow F = \frac{1}{3}\)
Tại C(4'1) thì F = - 3
Vậy F đạt giá trị nhỏ nhất tại C(4;1)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
