Chương 3: Nguyên Hàm - Tích Phân Và Ứng Dụng

Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại?

a)  \(e^{-x}\) và \(-e^{-x}\) ;                            

b) \(sin2x\) và  \(sin^2x\)

c) \((1-\frac{2}{x})^{2}e^{x}\)  và \((1-\frac{4}{x})e^{x}\)

Tìm nguyên hàm của các hàm số sau?

a) \(\small f(x)=\frac{x+\sqrt{x}+1}{^{\sqrt[3]{x}}}\).                            

b)  \(f(x)=\frac{2^{x}-1}{e^{x}}\).

c)  \(f(x)=\frac{1}{sin^{2}x.cos^{2}x}\).                         

d) \(f(x) = sin5x.cos3x\).

e) \(f(x) = tan^2x\).

g) \(f(x) = e^{3-2x}\).

h) \(f(x)=\frac{1}{(1+x)(1-2x)}\).

Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính:

a) \(\small \int xln(1+x)dx\).

b) \(\int (x^2+2x+1)e^xdx\).

c) \(\small \int xsin(2x+1)dx\).             

d) \(\small \int (1-x)cosxdx\).

Sử dụng phương pháp biến số, hãy tính:

a)  \(\small \int (1-x)^9dx\) (đặt u =1-x)

b)  \(\small \int x(1+x^2)^\frac{3}{2} dx\)​ (đặt u = 1 +  x²).

c)  \(\small \int cos^3x.sinxdx\) (đặt t = cosx).

d)  \(\int \frac{dx}{e^{x}+e^{-x}+2}\)  đặt u= e^x +1).

Tính các tích phân sau:

a)\(\int_{\frac{-1}{2}}^{\frac{1}{2}}\sqrt[3]{ (1-x)^{2}}dx\)                    b) \(\int_{0}^{\frac{\pi}{2}}sin(\frac{\pi}{4}-x)dx\)

c)                        d) 

e)                        g) 

Tính các tích phân sau:

a) \(\int_{0}^{2}\left | 1-x \right |dx\)                               b) \(\int_{0}^{\frac{\pi}{2}}sin^{2}x dx\)

c)                        d) 

Sử dụng phương pháp biến đổi số, tính tích phân:

a) \(\int_{0}^{3}\frac{x^{2}}{(1+x)^{\frac{3}{2}}}dx\)      (Đặt u= x+1) 

b)        (Đặt x = sint )

c)     (Đặt u = 1+x.e^x)

d)    (Đặt x= asint)

Sử dụng phương pháp tích phân tưng phần, hãy tính tích phân:

a)\(\int_{0}^{\frac{\pi}{2}}(x+1)sinxdx\)   ;      b) 

c)      ;       d)

Tính các tích phân sau:

a) \(\int_{0}^{1}(1+3x)^{\frac{3}{2}}dx\);        

b) \(\int_{0}^{\frac{1}{2}}\frac{x^{3}-1}{x^{2}-1}dx\);

c) .

Tính tích phân \(\int_{0}^{1}x(1-x)^{5}dx\) bằng hai phương pháp:

a) Đổi biến số u = 1 - x;

b) Tính tích phân từng phần.

Tính diện tích hình phẳng giới hạn bởi các đường:

a) \(y = x^2, y = x + 2\);   

b) \(y = |lnx|, y = 1\);

c) \(y = (x - 6)^2, y = 6x- x^2\)

Tính diện tích hình phẳng giới hạn bởi đường cong y = x² +1, tiếp tuyến với đường thẳng này tại điểm M(2;5) và trục Oy.

Parabol \(y=\frac{x^{2}}{2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2 \sqrt {2}\) thành hai phần. Tìm tỉ số diện tích của chúng.

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox:

a) \(\small y = 1 - x^2 , y = 0\) ;

b) \(\small y = cosx, y = 0, x = 0, x = \pi\) ;

c)  \(\small y = tanx, y = 0, x = 0,x=\frac{\pi }{4}\) ;

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt  \(\widehat{POA}=\alpha\) và \(OM=R, \left ( 0\leq \alpha \leq \frac{\pi }{3}, R>0 \right )\).

Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).

a) Tính thể tích của V theo α và R.      

b) Tìm \(\small \alpha\) sao cho thể tích V là lớn nhất.  

a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng.

b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.

a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.

b) Nêu các tính chất của tích phân. Cho ví dụ minh họa.

 Tìm nguyên hàm của các hàm số sau:

a) \(f(x)=(x-1)(1-2x)(1-3x)\)

b) \(f(x)=sin4xcos^22x\)
c) \(f(x)=\frac{1}{1-x^2}\)

c)\(f(x)=(e^x-1)^3\)

Tính:

a) \(\int (2-x)sinxdx\)

b) \(\frac{\int (x+1)^2}{\sqrt{x}}dx\)
c) \(\int \frac{e^{3x+1}}{e^x+1}dx\)
d) \(\int \frac{1}{(sinx+cosx)^2}dx\)
e) \(\int \frac{1}{\sqrt{1+x}+\sqrt{x}}dx\)
f) \(\int \frac{1}{(1+x)(2-x)}dx\)

Tính:
a) \(\int_{3}^{0}\frac{x}{\sqrt{1+x}}dx\)
b) \(\int_{1}^{64} \frac{1+\sqrt{x}}{\sqrt[3]{x}}dx\)
c) \(\int_{0}^{2} x^2.e^{3x}dx\)
d) \(\int_{0}^{\pi} \sqrt{1+sin2x}dx\)

Tính:

a) \(\int_{0}^{\frac{\pi}{2}}cos2xsin^2xdx\)

b) \(\int_{-1}^{1}\left | 2^2-2^{-x} \right |dx\)

c) \(\int_{-1}^{2} \frac{(x+1)(x+2)(x+3)}{x^2}dx\)

d) \(\int_{-1}^{\frac{\pi }{2}} (sinx+cosx)^2dx\)

e) \(\int_{-1}^{\pi } (x+sinx)^2dx\)

g) \(\int_{0}^{\pi }(x+sinx)^2dx\)

Xét hình phẳng D giới hạn bởi \(y=2\sqrt{1-x^2}\) và \(y=2(1-x)\)

a) Tính diện tích hình D

b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.

Tính \(\frac{\int dx}{\sqrt{1-x}}\) kết quả:

 (A). \(\frac{C}{ \sqrt{1-x}}\)                  (B) \(C\sqrt{1-x}\)

(C). \(-2\sqrt{1-x}+C\)      (D) \(\frac{2}{\sqrt{1-x}}+C\)

 Tính \(\int 2^{\sqrt{x}}.\frac{ln2}{\sqrt{x}}dx\), kết quả sai là:
(A) \(2^{\sqrt{x}+1}+C\)       

(B) \(2(2^{\sqrt{x}}-1)+C\)

(C) \(2(2^{\sqrt{x}}+1)+C\) 

(D) \(2^{\sqrt{x}}+C\)

 Tích phân \(\int_{0}^{\pi}cos^2x sinxdx\) bằng:
(A) \(-\frac{2}{3}\)          (B) \(\frac{2}{3}\)

(C)  \(\frac{3}{2}\)            (D) 

Cho hai tích phân \(\int_{0}^{\frac{\pi }{2}}sin^2xdx\) và \(\int_{0}^{\frac{\pi }{2}}cos^2x dx\). Hãy chỉ ra khẳng định đúng:

(A)  \(\int_{0}^{\frac{\pi }{2}}sin^2xdx >\int_{0}^{\frac{\pi }{2}}cos^2x dx\)
(B) \(\int_{0}^{\frac{\pi }{2}}sin^2xdx <\int_{0}^{\frac{\pi }{2}}cos^2x dx\)
(C) \(\int_{0}^{\frac{\pi }{2}}sin^2xdx =\int_{0}^{\frac{\pi }{2}}cos^2x dx\)

(D) Không so sánh được

Diện tích hình phẳng giới hạn bởi các đường cong:  

Câu a:  \(y=x^3\) và \(y=x^5\) bằng: 

(A). 0  

(B). -4

(C). \(\frac{1}{6}\) 

(D). 2

Câu b: \(y=x+sinx\) và \(y=x(0

(A). -4  

(B). 4

(C). 0  

(D). 1

Cho hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\) và \(y=x\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

(A). 

(B). \(-\pi\)

(C). \(\pi\)

(D). \(\frac{\pi}{6}\)

Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số 

\(f(x) = \frac{1}{{1 + \sin x}}?\)

a) \(F\left( x \right) = 1 - \cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right)\)

b) \(G(x) = 2\tan \frac{x}{2}\)

c) \(H(x) = \ln (1 + \sin x)\)

d) \(K(x) = 2\left( {1 - \frac{1}{{1 + \tan \frac{x}{2}}}} \right)\)

\(\mathop \smallint \nolimits x\ln (x + 1)dx\) bằng:

A. \(\left( {\frac{{{x^2}}}{2} - 1} \right)ln(x + 1) + \frac{1}{4}{(x - 1)^2} + C\)

B. \(\left( {\frac{{{x^2}}}{2} - 1} \right)\ln (x + 1) - \frac{1}{2}{(x - 1)^2} + C\)

C. \(\left( {\frac{{{x^2}}}{2} - \frac{1}{2}} \right)\ln (x + 1) - \frac{1}{4}{(x - 1)^2} + C\)

D. \(\left( {\frac{{{x^2}}}{2} + 1} \right)\ln (x + 1) - \frac{1}{4}{(x - 1)^2} + C\) 

Tính các tích phân sau bằng phương pháp đổi biến:

a) \(\int \limits_1^2 x{\left( {1 - x} \right)^5}dx\) (đặt  t = 1−x)

b) \(\int \limits_0^{\ln 2} \sqrt {{e^x} - 1} dx\) (đặt \(t = \sqrt {{e^x} - 1} \))

c) \(\int \limits_1^9 x\sqrt[3]{{1 - x}}dx\) (đặt \(t = \sqrt[3]{{1 - x}}\))

d) \(\int \limits_0^\pi  \frac{{x\sin x}}{{1 + {{\cos }^2}x}}dx\)    (đặt \(x = \pi  - t\))

e) \(\int \limits_{ - 1}^1 {x^2}{\left( {1 - {x^3}} \right)^4}dx\)

Áp dụng phương pháp tích phân từng phần, hãy tính các tích phân sau:

a) \(\int \limits_0^{\frac{\pi }{2}} x\cos 2xdx\)

b) \(\int \limits_0^{\ln 2} x{e^{ - 2x}}dx\)

c) \(\int \limits_0^1 \ln (2x + 1)dx\)

d) \(\int\limits_2^3 {\left[ {\ln \left( {x - 1} \right)} \right] - \ln \left( {x + 1} \right)dx} \)

e) \(\int \limits_{\frac{1}{2}}^2 \left( {1 + x - \frac{1}{x}} \right){e^{x + \frac{1}{x}}}dx\)

g) \(\int \limits_0^{\frac{\pi }{2}} x\cos x{\sin ^2}xdx\)

Tính các tích phân sau đây:

a) \(\int \limits_0^{\frac{\pi }{2}} \left( {x + 1} \right)\cos \left( {x + \frac{\pi }{2}} \right)dx\)

b) \(\int \limits_0^1 \frac{{{x^2} + x + 1}}{{x + 1}}{\log _2}\left( {x + 1} \right)dx\)

c) \(\int \limits_{\frac{1}{2}}^1 \frac{{{x^2} - 1}}{{{x^4} + 1}}dx\)

d) \(\int \limits_0^{\frac{\pi }{2}} \frac{{\sin 2xdx}}{{3 + 4\sin x - \cos 2x}}\)                                           

Chứng minh rằng hàm số f(x) cho bởi \(\int \limits_0^x \frac{t}{{\sqrt {1 + {t^4}} }}dt,x \in R\) là hàm số chẵn.

Giả sử hàm số f(x) liên tục trên đoạn [-a;a]. Chứng minh rằng

\(\int \limits_{ - a}^a f\left( x \right)dx = \left\{ \begin{array}{l}
2\int \limits_0^a f\left( x \right)\\
0
\end{array} \right.\)

nếu \(f\) chẵn hoặc \(f\) lẻ.

Áp dụng để tính \(\int \limits_{ - 2}^2 \ln \left( {x + \sqrt {1 + {x^2}} } \right)dx\)

Giả sử hàm số f(x) liên tục trên đoạn [a;b]. Chứng minh rằng

\(\int \limits_0^{\frac{\pi }{2}} f\left( {\sin x} \right)dx = \int \limits_0^{\frac{\pi }{2}} f\left( {\cos x} \right)dx\)

Đặt \({I_n} = \int \limits_0^{\frac{\pi }{2}} {\sin ^n}xdx,n \in {N^ * }.\)

a) Chứng minh rằng \({I_n} = \frac{{n - 1}}{n}{I_{n - 2}},n > 2\)

b) Tính I₃ và I₅

Hãy chỉ ra kết quả sai trong việc khử giá trị tuyệt đối của tích phân sau đây:

\(\int \limits_0^{2\pi } \left| {\sin x} \right|dx\)

A. \(\int \limits_0^{2\pi } \sin xdx\)                            

B. \(\int \limits_0^\pi  2\sin xdx\)

C. \(\int \limits_0^\pi  \sin xdx - \int \limits_0^{2\pi } \sin xdx\)    

D. \( - \int \limits_\pi ^{2\pi } 2\sin xdx\)

\(\int \limits_{ - 1}^1 \left| {x - {x^3}} \right|dx\) bằng:

A. \(\frac{1}{2}\)

B. 2

C. -1

D. 0

\(\int \limits_1^e \frac{{\ln x}}{{{x^2}}}dx\) bằng?

A. \( - 1 - \frac{1}{e}\)

B. \(1 - \frac{2}{e}\)

C. \( - 1 + \frac{2}{e}\)

D. 0

\(\int \limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} \left( {\frac{{\sin 2x\sin x}}{2} + {{\cos }^3}x} \right)dx\) bằng

A. 2 

B. \(2\pi \)

C. \(\pi \)$$

D. \(-\pi \)

Đối với tích phân \(\int \limits_0^{\frac{\pi }{4}} \frac{{\tan x}}{{{{\cos }^2}x}}dx\), thực hiện đổi biến số \(t = \tan x\), ta được:

A. \(\int \limits_0^{\frac{\pi }{4}} tdt\)

B. \(\int \limits_{ - 1}^0 tdt\)

C. \(\int \limits_0^1 tdt\)

D. \( - \int \limits_0^1 tdt\)

\(\int \limits_0^1 \sin \sqrt x dx\) bằng

A. \(2(\sin 1 - \cos 1)\)

B. \(2(\cos 1 - \sin 1)\)

C. \(\sin 1 - \cos 1\)

D. \(2(\sin 1 + \cos 1)\)

Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) \(y = 2x - {x^2},x + y = 2\);

b) \(y = {x^3} - 12x,y = {x^2}\);

c) \(x + y = 1,x + y =  - 1,x - y = 1,x - y =  - 1\);

d) \(y = \frac{1}{{1 + {x^2}}},y = \frac{1}{2}\);

e) \(y = {x^3} - 1\) và tiếp tuyến với \(y = {x^3} - 1\) tại điểm (-1;-2).

Tìm nguyên hàm của các hàm số sau :

\(\begin{array}{l}
a)f\left( x \right) = 3{x^2} + \frac{x}{2}\\
b)f(x) = 2{x^3} - 5x + 7\\
c)f\left( x \right) = \frac{1}{{{x^2}}} - {x^2} - \frac{1}{3}\\
d)f(x) = {x^{ - \frac{1}{3}}}\\
e)f(x) = {10^{2x}}
\end{array}\)

Tìm

\(\begin{array}{*{20}{l}}
{a)\int {\left( {\sqrt x  + \sqrt[3]{x}} \right)dx} }\\
{b)\int {\frac{{x\sqrt x  + \sqrt x }}{{{x^2}}}} dx}\\
{c)\int {4{{\sin }^2}xdx} }\\
{d)\int {\frac{{1 + \cos 4x}}{2}dx} }
\end{array}\)

Chọn khẳng định đúng trong các khẳng định dưới đây :

Nguyên hàm của hàm số \(y = x\sin ⁡x\) là

\(\begin{array}{*{20}{l}}
{(A){x^2}\sin \frac{x}{2} + C}\\
{(B) - x\cos x + C}\\
{(C) - x\cos x + \sin x + C}
\end{array}\)

Khẳng định sau đúng hay sai :

Nếu \(f\left( x \right) = {\left( {1 - \sqrt x } \right)^\prime }\) thì \(\smallint f(x)dx =  - \sqrt x  + C\)

Dùng phương pháp đổi biến số, tìm nguyên hàm của các hàm số sau:

\(\begin{array}{l}
a)f\left( x \right) = \frac{{9{x^2}}}{{\sqrt {1 - {x^3}} }}\\
b)f(x) = \frac{1}{{\sqrt {5x + 4} }}\\
c)f(x) = x\sqrt[4]{{1 - {x^2}}}\\
d)f(x) = \frac{1}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}
\end{array}\)

Dùng phương pháp lấy số nguyên hàm từng phần, tìm nguyên hàm của các hàm số sau:

\(\begin{array}{l}
a)f\left( x \right) = x\sin x\frac{x}{2}\\
b)f(x) = {x^2}cosx\\
c)f(x) = x{e^x}\\
d)f(x) = {x^3}lnx
\end{array}\)

Tìm nguyên hàm của các hàm số sau:

\(\begin{array}{*{20}{l}}
{a)f\left( x \right) = 3x\sqrt {7 - 3{x^2}} }\\
{b)f\left( x \right) = \cos \left( {3x + 4} \right)}\\
{c)f\left( x \right) =  - \frac{1}{{{{\cos }^2}\left( {3x + 2} \right)}}}\\
{d)f(x) = {{\sin }^5}\frac{x}{3}\cos \frac{x}{3}}
\end{array}\)

Tìm nguyên hàm của các hàm số sau:

\(\begin{array}{l}
a)f\left( x \right) = {x^2}\left( {\frac{{{x^3}}}{{18}} - 1} \right)\\
b)f\left( x \right) = \frac{1}{{{x^2}}}{\rm{sin}}\frac{1}{x}\cos \frac{1}{x}\\
c)f\left( x \right) = {x^3}{e^x}\\
d)f(x) = {e^{\sqrt {3x - 9} }}
\end{array}\)

Tìm nguyên hàm của các hàm số sau:

\(\begin{array}{l}
a)f\left( x \right) = {x^2}\cos 2x\\
b)f\left( x \right) = \sqrt x \ln x\\
c)f\left( x \right) = {\sin ^4}x\cos x\\
d)f(x) = x\cos ({x^2})
\end{array}\)

Không tìm nguyên hàm hãy tính các tích phân sau:

\(\begin{array}{l}
a)\int\limits_{ - 2}^4 {\left( {\frac{x}{2} + 3} \right)dx} \\
b)\int \limits_{ - 1}^2 \left| x \right|dx\\
c)\int \limits_{ - 3}^3 \sqrt {9 - {x^2}} dx
\end{array}\)

Cho biết \(\int \limits_1^2 f\left( x \right)dx =  - 4,\int\limits_1^5 {f(x)dx}  = 6,\int\limits_1^5 {g(x)dx}  = 8.\) Hãy tính

\(\begin{array}{l}
a)\int\limits_2^5 {f(x)dx} \\
b)\int\limits_1^2 {3f(x)dx} \\
c)\int\limits_1^5 {\left[ {f(x) - g(x)} \right]dx} \\
d)\int\limits_1^5 {\left[ {4f(x) - g(x)} \right]dx} 
\end{array}\)

Cho biết \(\lint \limits_0^3 f\left( z \right)dz = 3,\int \limits_0^4 f\left( x \right)dx = 7.\). Hãy tính \(\int \limits_3^4 f\left( t \right)dt.\)

a) Chứng minh rằng nếu \(f(x) \ge 0\) trên [a; b] thì \(\int \limits_a^b f\left( x \right)dx \ge 0.\)

b) Chứng minh rằng nếu \(f(x) \ge g(x)\) trên [a; b] thì \(\int \limits_a^b f\left( x \right)dx \ge \int \limits_a^b g\left( x \right)dx\)

a) Một vật chuyển động với vận tốc v(t) = 1 − 2sin2t (m/s). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm t = 0 (s) đến thời điểm \(t = \frac{{3\pi }}{4} \left( s \right)\)

b) Một vật chuyển động chậm dần với vận tốc v(t) = 160 − 10t (m/s). Tính quãng đường mà vật di chuyển được từ thời điểm t = 0 đến thời điểm mà vật dừng lại. 

Một vật đang chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc a = 3t + t² (m/s²). Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tang tốc.

Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu 25 m/s. gia tốc trọng trường là 9,8m/s²

a) Sau bao lâu viên đạn đạt tới vận tốc cao nhất.

b) Tính quãng đường viên đạn đi được tính từ lúc bắn lên cho đến khi rơi xuống đất.

Dùng phương pháp đổi biến số tính các tích phân sau:

\(\begin{array}{l}
a)\int \limits_0^1 \sqrt {x + 1} dx\\
b)\int \limits_0^{\frac{\pi }{4}} \frac{{\tan x}}{{{{\cos }^2}x}}dx\\
c)\int \limits_0^1 {t^3}{\left( {1 + {t^4}} \right)^3}dt\\
d)\int \limits_0^1 \frac{{5x}}{{{{\left( {{x^2} + 4} \right)}^2}}}dx\\
e)\int \limits_0^{\sqrt 3 } \frac{{4x}}{{\sqrt {{x^2} + 1} }}dx\\
f)\int \limits_0^{\frac{\pi }{6}} \left( {1 - \cos 3x} \right)\sin 3xdx
\end{array}\)

Dùng phương pháp tích phân từng phần để tính các tích phân sau:

\(\begin{array}{l}
a)\int \limits_1^2 {x^5}\ln xdx\\
b)\int \limits_0^1 \left( {x + 1} \right){e^x}dx\\
c)\int \limits_0^\pi  {e^x}\cos xdx\\
d)\int \limits_0^{\frac{\pi }{2}} x\cos xdx
\end{array}\)

Tính 

\(\begin{array}{l}
a)\int \limits_0^1 \sqrt {{t^5} + 2t} \left( {2 + 5{t^4}} \right)dt\\
b)\int \limits_0^{\frac{\pi }{2}} x\sin {\rm{xcosx}}dx
\end{array}\)

Tính 

\(\begin{array}{l}
a)\int \limits_0^\pi  5{\left( {5 - 4\cos t} \right)^{\frac{1}{4}}}\sin tdt\\
b)\int \limits_0^{\sqrt 3 } \frac{{{x^3}dx}}{{\sqrt {{x^2} + 1} }}
\end{array}\)

Giả sử F là một nguyên hàm của hàm số \(y = \frac{{\sin x}}{x}\) trên khoảng \((0; + \infty )\). Khi đó \(\int \limits_1^3 \frac{{\sin 2x}}{x}dx\) là

(A) F(3) − F(1)                 

(B) F(6) − F(2)                

(C) F(4) − F(2)                 

D) F(6) − F(4)   

Chứng minh rằng

\(\begin{array}{l}
a)\int \limits_0^1 f\left( x \right)dx = \int \limits_0^1 f\left( {1 - x} \right)dx\\
b)\int \limits_{ - 1}^1 f\left( x \right)dx = \int \limits_0^1 \left[ {f\left( x \right) + f\left( { - x} \right)} \right]dx
\end{array}\)

Cho \(\int \limits_0^1 f\left( x \right)dx = 3.\) Tính \(\int \limits_{ - 1}^0 f\left( x \right)dx\) trong các trường hợp sau:

a) f là hàm số lẻ;                               

b) f là hàm số chẵn.

Tính các tích phân sau:

\(\begin{array}{l}
a)\int\limits_1^2 {{x^2}{e^{{x^3}}}dx} \\
b)\int \limits_1^3 \frac{1}{x}{\left( {\ln x} \right)^2}dx\\
c)\int \limits_0^{\sqrt 3 } x\sqrt {1 + {x^2}} dx\\
d)\int \limits_0^1 {x^2}{e^{3{x^3}}}dx\\
e)\int \limits_0^{\frac{\pi }{2}} \frac{{\cos x}}{{1 + {\rm{sinx}}}}dx
\end{array}\)

Tính các tích phân sau :

\(\begin{array}{l}
a)\int \limits_0^{\frac{\pi }{4}} x\cos 2xdx\\
b)\int \limits_0^1 \frac{{\ln \left( {2 - x} \right)}}{{2 - x}}dx\\
c)\int \limits_1^{\frac{\pi }{2}} {x^2}\cos xdx.\\
d)\int \limits_0^{\frac{\pi }{4}} x\cos 2xdx\\
e)\int \limits_1^e {x^2}\ln xdx
\end{array}\)

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sinx + 1, trục hoành và hai đường thẳng x = 0 và \(x = \frac{{7\pi }}{6}\) 

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hàm số y = cos²x trục hoành, trục tung và đường thẳng x = π
b) Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \sqrt[3]{x}\)
c) Đồ thị hàm số y = 2x² và y = x⁴ −2x² trong miền x ≥ 0 .

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị các hàm số y = x² − 4, y = −x² − 2x và đường thẳng x = −3, x = −2
b) Đồ thị hai hàm số y = x² và y = −x² − 2x
c) Đồ thị hàm số y = x³ − 4x, trục hoành, đường thẳng x = - 2 và đường thẳng x = 4

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = −1 và x = 1, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−1 ≤ x ≤ 1) là một hình vuông cạnh là \(2\sqrt {1 - {x^2}} \) 

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ π) là một tam giác đều cạnh \(2\sqrt {{\rm{sinx}}} \)

Cho hình phẳng A giới hạn bởi các đường y = 0$, \mathrm{x }= 4$, và \(y = \sqrt x  - 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành

Cho hình phẳng B giới hạn bởi các đường x = 2/y, y = 1 và y = 4. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung

Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt 5 {y^2},x = 0,y =  - 1\) và y = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị các hàm số y = x, y = 1 và \(y = \frac{{{x^2}}}{4}\) trong miền x ≥ 0, y ≤ 1.

b) Đồ thị hai hàm số y = x⁴ − 4x² + 4, y = x², trục tung và đường thẳng x = 1

c) Đồ thị các hàm số y = x², y = 4x − 4 và y = −4x – 4

Tính diện tích hình phẳng giới hạn bởi:

a) Đồ thị hai hàm số y = x² + 1 và y = 3 – x

b) Các đường có phương trình x = y³, y = 1, và x = 8

c) Đồ thị của hàm số \(y = \sqrt x \),y = 6 − x và trục hoành.

Tính thể tích của vật thể T nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π) là một hình vuông cạnh là \(2\sqrt {\sin x} \)

Cho hình phẳng A giới hạn bởi các đường y = x², x = 0 và x = 2. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng A giới hạn bởi các đường y = cosx,y = 0, x = 0 và x = π/4. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{\frac{x}{2}}}\) y = 0, x = 0 và x = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt {2\sin 2y} ,x = 0,y = 0\), x = 0,y = 0, \(y = \frac{\pi }{2}\). Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.

Tìm nguyên hàm của các hàm số sau:

\(\begin{array}{*{20}{l}}
{a)y = 2x(1 - x - 3)}\\
{b)y = 8x - \frac{2}{{{x^{\frac{1}{4}}}}}}\\
{c)y = {x^{\frac{1}{2}}}\sin \left( {{x^{\frac{3}{2}}} + 1} \right)}\\
{d)y = \frac{{\sin (2x + 1)}}{{{{\cos }^2}(2x + 1)}}}
\end{array}\)

Tìm nguyên hàm của các hàm số sau:

\(\begin{array}{l}
a)y = \frac{1}{{{x^2}}}\cos \left( {\frac{1}{x} - 1} \right)\\
b)y = {x^3}{\left( {1 + {x^4}} \right)^3}\\
c)y = \frac{{x{e^{2x}}}}{3}\\
d)y = {x^2}{e^x}
\end{array}\)

Tìm nguyên hàm của các hàm số sau:

a. y =  x.e^-x

b. \(y = \frac{{\ln x}}{x}\)

Tìm hàm số y = f(x) nếu biết dy = 12x(3x² − 1)³dx và f(1) = 3

Xác định số b dương để tích phân \(\int\limits_0^b {(x - {x^2})dx} \) có giá trị lớn nhất.

Cho biết \(\int\limits_7^9 {f(x)dx}  =  - 1,\)

\(\int\limits_7^9 {f(x)dx}  = 5,\int\limits_7^9 {g(x)dx}  = 4.\)

Hãy tìm:

\(\begin{array}{l}
a)\int \limits_1^9  - 2f\left( x \right)dx\\
b)\int \limits_7^9 \left[ {f\left( x \right) + g\left( x \right)} \right]dx\\
c)\int\limits_7^9 {[2f(x) - 3g(x)]dx} \\
d)\int\limits_1^7 {f(x)dx} 
\end{array}\)

Cho hàm số f liên tục trên [a; b]. Tỉ số: \(\frac{1}{{b - a}} - \int_a^b {f(x)dx} \) được gọi là giá trị trung bình của hàm số f trên [a;b] và được kí hiệu là m(f). Chứng minh rằng tồn tại điểm c ∈ [a; b] sao cho m(f) = f(c)

Giả sử một vật từ trạng thái nghỉ khi t = 0 (s) chuyển động thẳng với vận tốc v(t) = t(5 − t) (m/s). Tìm quãng đường vật đi được cho tới khi nó dừng lại.

Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.

Tính các tích phân sau:

\(\begin{array}{l}
a)\int_0^{\frac{\pi }{2}} {{x^2}sin2xdx} \\
b)\int_1^2 {x(2{x^2} + 1)dx} \\
c)\int_2^3 {(x - 1){e^{{x^2} - 2x}}dx} 
\end{array}\)

Tính diện tích các hình phẳng giới hạn bởi:

a) Đồ thị các hàm số y = 4 − x²; y = -x + 2

b) Các đường cong có phương trình x = 4 − 4y² và x = 1 − y⁴ trong miền x ≥ 0.

Tính diện tích của các hình phẳng giới hạn bởi:

a) Parabol y = x² − 2x + 2, tiếp tuyến của nó tại điểm M(3; 5) và trục tung

b) Parabol y = −x² + 4x − 3y và các tiếp tuyến của nó tại các điểm A(0;−3) và B(3;0)

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bơi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ (0 ≤ x ≤ 2) là một nửa hình tròn đường kính \(\sqrt 5 {x^2}\)

Xét hình phẳng giới hạn bởi đường hypebol y = 2/x và các đường thẳng y = 1, y = 4, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng đó quanh trục tung.

Cho hình phẳng A được giới hạn bởi đồ thị hàm số: \(y = \sqrt {\cos x} \left( {0 \le x \le \frac{\pi }{2}} \right)\) và hai trục tọa độ. Tính thể tích khối tròn xoay tọa thành khi quay hình đó quay trục tung.

Cho hình phẳng A được giới hạn bởi đường cong có phương trình x(y + 1) = 2 và các đường thẳng x = 0, y = 0, y = 3. Tính thể tích khối tròn xoay tạo được khi quay A quanh trục tung.

Cho hình phẳng A được giới hạn bởi đường cong có phương trình x − y² = 0 và các đường thẳng y = 2, x = 0. Tính thể tích khối tròn xoay tạo thành khi quay A.

a) Quanh trục hoành;

b) quanh trục tung

Cho hình phẳng A được giới hạn bởi đường cong có phương trình \(y = {x^{\frac{1}{2}}}{e^{\frac{x}{2}}}\) và các đường thẳng x = , x = 2, y = 0.Tính thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành.

Cho hình phẳng A được giới hạn bởi đường cong có phương trình y² = x³ và các đường thẳng y = 0, x = 1. Tính thể tích khối tròn xoay tạo được khi quay A

a) Quanh trục hoành      

b) Quanh trục tung.

Tính thể tích vật thể:

a) Có đáy là một tam giác cho bởi: y = x , y = 0 , và x = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

b) Có đáy là một hình tròn giới hạn bởi x² + y² = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:

a) y = 2 – x², y = 1, quanh trục Ox.

b) y = 2x – x², y = x, quanh trục Ox.

c) \(y = {(2x + 1)^{\frac{1}{3}}},x = 0,y = 3\) quanh trục Oy.

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y = \frac{1}{x}\), y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi \(a \to  + \infty \) (tức là \(\mathop {\lim }\limits_{a \to  + \infty } V(a)\)).

Một hình phẳng được giới hạn bởi ${\displaystyle \mathrm{}}$\(y = {e^{ - x}},y = 0,x = 0,x = 1\). Ta chia đoạn [0;1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như dưới).

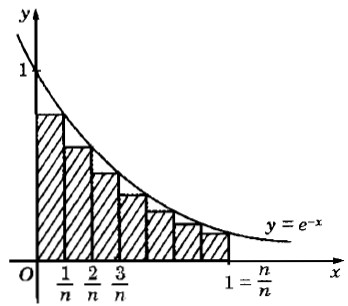
a) Tính diện tích S_n của hình bậc thang (tổng diện tích của n hình chữ nhật con).

b) Tìm \(\mathop {\lim }\limits_{n \to \infty } {S_n}\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.

Cho hình phẳng R giới hạn bởi các đường sau đây: \({y_1} = {f_1}\left( x \right).{y_2} = {f_2}\left( x \right)\) (\({f_1},{f_2}\) là các hàm số liên tục trên đoạn [a;b]), x = a và x = b. Hãy chỉ ra công thức sai trong việc tính diện tích hình R.

A. \(\int \limits_a^b \left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx\)

B. \(\int \limits_a^b \left| {{f_2}\left( x \right) - {f_1}\left( x \right)} \right|dx\)

C. \(\left| {\int \limits_a^b \left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \right|\)

D. \(\left| {\int \limits_a^b \left[ {{f_1}\left( x \right) - {f_2}\left( x \right)} \right]dx} \right|\)

Diện tích hình phẳng P giới hạn bởi các đường \({y_1} = x,{y_2} = 2x,{y_3} = 2 - x\) bằng:

A. 1                      

B. \(\frac{2}{3}\)

C. 2                     

D. \(\frac{2}{3}\)

Diện tích của hình phẳng giới hạn bởi các đường \({y_1} = {x^3};{y_2} = 4x\) bằng

A. 0                   

B. 4

C. 8                   

D. −8

Cho hình phẳng H giới hạn bởi các đường y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b;a]). Thể tích khối tròn xoay tạo nên bởi phép quay hình H quanh trục Ox được cho bởi công thức:

A. \(\pi \int \limits_a^b {f^2}\left( x \right)dx\)   

B. \(\int \limits_a^b {f^2}\left( x \right)dx\)

C. \(\pi \int \limits_b^a {f^2}\left( x \right)dx\)

D. \(\int \limits_a^b {\left[ {\pi f\left( x \right)} \right]^2}dx\)

Quay hình phẳng Q giới hạn bởi các đường \({y_1} = \sin x,{y_2} = \frac{{2x}}{\pi }\) quanh trục Ox, ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

A. \(\frac{1}{6}\)                    

B. \(\frac{\pi }{6}\)

C. 8                      

D. \(\frac{{{\pi ^2}}}{6}\)

Quay hình phẳng G giới hạn bởi các đường y = x³, y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:

A. \(\pi \)                   

B. \(\frac{5}{3}\pi \)${\displaystyle }$

C. \(\frac{3}{5}\pi \)               

D. \(\frac{3}{5}\)${\displaystyle \frac{\mathrm{}}{}}$

Tính các tích phân sau:

a) \(\int \limits_0^1 {(y - 1)^2}\sqrt y dy\), đặt \(t = \sqrt y \)

b) \(\int \limits_1^2 ({z^2} + 1)\sqrt[3]{{{{(z - 1)}^2}}}dz\), đặt \(u = \sqrt[3]{{{{(z - 1)}^2}}}\)

c) \(\int \limits_1^e \frac{{\sqrt {4 + 5\ln x} }}{x}dx\)

d) \(\int \limits_0^{\frac{\pi }{2}} ({\cos ^5}\varphi  - {\sin ^5}\varphi )d\varphi \)

Tính diện tích các hình phẳng giới hạn bởi các đường sau:

a) \(y = x - 1 + \frac{{\ln x}}{x},y = x - 1\) và x = e;

b) \(y = {x^3} - {x^2}\) và \(y = \frac{1}{9}(x - 1)\);

Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi

a) \(y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ x = 1, quanh trục Oy;

b) \(y = \frac{1}{x} - 1,y = 0,y = 2x\), quanh trục Ox.

c) \(y = \left| {2x - {x^2}} \right|,y = 0\) và x = 3, quanh :

* Trục Ox

* Trục Oy

Hãy chỉ ra các kết quả đúng trong các kết quả sau:

a) \(\int \limits_0^1 {x^n}{(1 - x)^m}dx = \int \limits_0^1 {x^m}{(1 - x)^n}dx;m,n \in {N^ * }\)

b) \(\int \limits_{ - 1}^1 \frac{{{t^2}}}{{{e^t} + 1}}dt = \int \limits_0^1 {t^2}dt\)

c) \(\int \limits_0^1 {\sin ^3}x\cos xdx = \int \limits_0^1 {t^3}dt\)

Hàm số nào dưới đây không là nguyên hàm của hàm số \(f\left( x \right) = \frac{{x\left( {2 + x} \right)}}{{{{\left( {x + 1} \right)}^2}}}\)?

A. \(\frac{{{x^2} + x - 1}}{{x + 1}}\)      

B. \(\frac{{{x^2} - x - 1}}{{x + 1}}\)

C. \(\frac{{{x^2} + x + 1}}{{x + 1}}\)   

D. \(\frac{{{x^2}}}{{x + 1}}\)

Nếu \(\int \limits_a^d f\left( x \right)dx = 5,\int \limits_b^d f\left( x \right)dx = 2\)

với a < d < b thì \(\int \limits_a^b f\left( x \right)dx\) bằng

A. - 2

B. 8

C. 0

D. 3

Tìm khẳng định sai trong các khẳng định sau:

A. \(\int \limits_0^1 \sin \left( {1 - x} \right)dx = \mathop \smallint \limits_0^1 \sin xdx\)

B. \(\int \limits_0^\pi  \sin \frac{x}{2}dx = 2\mathop \smallint \limits_0^{\frac{\pi }{2}} \sin xdx\)

C. \(\int \limits_0^1 {\left( {1 + x} \right)^x}dx = 0\)

D. \(\int \limits_{ - 1}^1 {x^{2007}}\left( {1 + x} \right)dx = \frac{2}{{2009}}\)

Tìm khẳng định đúng trong các khẳng định sau:

A. \(\int \limits_0^\pi  \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi  \left| {\sin \left( {x - \frac{\pi }{4}} \right)} \right|dx\)

B. \(\int \limits_0^\pi  \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = \int \limits_0^\pi  \left| {\cos \left( {x + \frac{\pi }{4}} \right)} \right|dx\)

C. \(\begin{array}{l}
\int \limits_0^\pi  \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx\\
 = \int \limits_0^{\frac{{3\pi }}{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx - \int \limits_{\frac{{3\pi }}{4}}^\pi  \sin \left( {x + \frac{\pi }{4}} \right)dx
\end{array}\)

D. \(\int \limits_0^\pi  \left| {\sin \left( {x + \frac{\pi }{4}} \right)} \right|dx = 2\int \limits_0^{\frac{\pi }{4}} \sin \left( {x + \frac{\pi }{4}} \right)dx\)

\(\int \limits_0^1 x{e^{1 - x}}dx\) bằng

A. 1 - e

B. e - 2

C. 1

D. - 1

Nhờ ý nghĩa hình học của tích phân, hãy tìm khẳng định sai trong các khẳng định sau:

A. \(\int \limits_0^1 \ln \left( {1 + x} \right)dx > \int \limits_0^1 \frac{{x - 1}}{{e - 1}}dx\)

B. \(\int \limits_0^{\frac{\pi }{4}} {\sin ^2}xdx < \int \limits_0^{\frac{\pi }{4}} \sin 2xdx\)

C. \(\int \limits_0^1 {e^{ - x}}dx > \int \limits_0^1 {\left( {\frac{{1 - x}}{{1 + x}}} \right)^2}dx\)

D. \(\int \limits_0^1 {e^{ - {x^2}}}dx > \int \limits_0^1 {e^{ - {x^3}}}dx\)

Thể tích của khối tròn xoay tạo nên do quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y = {\left( {1 - x} \right)^2},y = 0\), x = 0 và x = 2 bằng

A. \(\frac{{8\pi \sqrt 2 }}{3}\)             

B. \(\frac{{2\pi }}{5}\)

C. \(\frac{{5\pi }}{2}\)                   

D. \(2\pi \)

\(\int \limits_{ - \frac{1}{2}}^{\frac{1}{2}} \frac{{x\left( {1 + {x^2} + {x^4}} \right)}}{{1 + {x^2}}}dx\) bằng

A. 0

B. 1

C. - 1

D. 2

Khẳng định nào sau đây sai?

A. \(\int \limits_{\frac{\pi }{2}}^\pi  \frac{{\sin x}}{x}dx < \int \limits_{\frac{\pi }{2}}^\pi  \frac{{\cos x}}{x}dx\)

B. \(\int \limits_{\frac{\pi }{4}}^1 \frac{{\tan x}}{x}dx > \int \limits_{\frac{\pi }{4}}^1 \frac{{\cot x}}{x}dx\)

C. \(\int \limits_0^{\frac{\pi }{4}} {\sin ^4}xdx < \int \limits_0^{\frac{\pi }{2}} dx\)

D. \(\int \limits_1^e \frac{{\ln x}}{x}dx < \int \limits_1^e \frac{{{e^x}}}{x}dx\)

Diện tích của hình phẳng được giới hạn bởi các đường \(y = \tan x,y = 0,x =  - \frac{\pi }{4}\) và \(x = \frac{\pi }{4}\) bằng

A. \( \pi \)         

B. \( - \pi \)

C. \(\ln 2\)                     

D. 0

Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường \(y = {\sin ^{\frac{3}{2}}}x,y = 0,x = 0\) và \(x = \frac{\pi }{2}\) bằng

A. 1

B. \(\frac{2}{7}\)

C. \(2\pi \)

${\displaystyle }$D. \(\frac{2}{3}\pi \)

Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) =  - 5t + 10\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển bao nhiêu mét?

A. 0,2m

B. 2m

C. 10m

D. 20m

Giả sử \(\int\limits_1^5 {\frac{{dx}}{{2x - 1}}}  = \ln c\). Giá trị của c là
(A) 9

(B) 3

(C) 81

(D) 8

Giá trị của $\mathrm{\backslash (\backslash int\; \backslash limits\_0^2\; 2\{e^\{2x\}\}dx\backslash )}$ là

(A) \({e^4}\)

(B) \({e^4} - 1\)

(C) \(4{e^4}\)

(D) \(3{e^4} - 1\)

Giá trị của \(\int \limits_{ - 1}^0 {x^2}{\left( {x + 1} \right)^3}dx\) là:

(A) \( - \frac{7}{{10}}\)

(B) \( - \frac{6}{{10}}\)

(C) $$\(\frac{2}{{15}}\)

(D) \(\frac{1}{{60}}\)

Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng y = 4x và đồ thị hàm số y = x³ là:

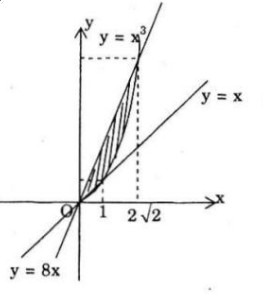
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bới hai đường thẳng \(y = 8x,y = x\) và đồ thị hàm số \(y = {x^3}\) là:

(A) 12$$

(B) 15,75$\mathrm{}$

(C) 6,75$\mathrm{}$

(D) 4

Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bởi đường thẳng y = 2x và đồ thị hàm số y = x² là:

(A) \(\frac{4}{3}\)

(B) \(\frac{3}{2}\)

(C) \(\frac{5}{3}\)

(D) \(\frac{{23}}{{15}}\)

Cho hình phẳng A được giới hạn bởi đồ thị hàm hai số \(y = {x^2}\) và \(y = 6 - \left| x \right|\). Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung:

(A) \(\frac{{32\pi }}{3}\)

(B) \(9\pi \)

(C) \(8\pi \)

(D) \(\frac{{20\pi }}{3}\)

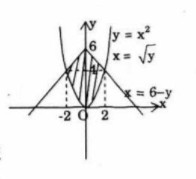
Cho a, b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai được giới hạn bởi parabol y = ax² và đường thẳng y = −bx. Biết rằng thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc vào giá trị của a và b. Khi đó a và b thỏa mãn điều kiện sau:

(A) \({b^4} = 2{a^5}\)

(B) \({b^3} = 2{a^5}\)

(C) \({b^5} = 2{a^3}\)

(D) \({b^4} = 2{a^2}\)