Bài tập 7 trang 127 SGK Giải tích 12

Bài tập 7 trang 127 SGK Giải tích 12

Câu a:

Xét hàm số: \(y=2\sqrt{1-x^2}\)

Tập xác định: \(D=[-1;1]; y'=\frac{-2x}{\sqrt{1-x^2}}\)

Dấu của y' như sau: 

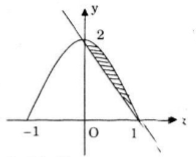
Vì thế đường cong \(y=2\sqrt{1-x^2}\) và đường thẳng \(y=2(1-x)\) được vẽ trong cùng một hệ trục toạ độ Oxy như sau:

Hình D là "miền gạch sọc" trong hình vẽ trên.

Ta có diện tích hình D là:

\(S_D=\int_{0}^{1}\left | 2\sqrt{1-x^2} -2(1-x)\right |dx\)

Ta sẽ chứng minh: \(\sqrt{1-x^2}\geq 1-x \ \ * \ \forall x\in D_1=[0;1]\)

Thật vậy, \(\forall x\in D_1\) thì \(\Leftrightarrow 1-x\geq (1-x^2)\Leftrightarrow 2x^2-2x\leq 0\)

\(\Leftrightarrow x(x-1)\leq 0 \ (**)\)

Bất đẳng thức (**) hiển nhiên đúng \(\forall x\in D_1\)

Vậy (*) đúng \(\forall x\in D_1\). Do (*) nên:

\(S_D=\int_{0}^{1}\left [ 2\sqrt{1-x^2}-2(1-x) \right ]dx\)

\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-2 \int_{0}^{1}dx+2\int_{0}^{1}x dx\)

\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-2x \Bigg|^1_0+x^2\Bigg|^1_0\)

\(\Leftrightarrow S_D=2\int_{0}^{1} \sqrt{1-x^2}dx-1.\)

Đặt x = sint (với \(t\in \left ( 0;\frac{\pi }{2} \right )\)) ta có:

dx = cos t dt, đổi cận:

Cho nên: \(\int_{0}^{1} \sqrt{1-x^2}dx=\int_{0}^{\frac{\pi }{2}} cos^2 t dt=\int_{0}^{1} \frac{1+cos 2t}{2}dt\)

\(=\frac{1}{2}\int_{0}^{\frac{\pi }{2}} dt+\frac{1}{2}\int_{0}^{\frac{\pi }{2}} cos2t dt= \frac{\pi }{4}-\frac{1}{4}sin 2t \Bigg|_{0}^{\frac{\pi }{2}}= \frac{\pi }{4}\)

Vậy: \(S_D=\frac{\pi }{2}-1\)

Câu b:

Gọi V; V₁; V₂ lần lượt là thể tích khối tròn xoay tạo thành khi quay D; hình phẳng giới hạn bởi giới hạn bởi các đường \(y=2\sqrt{1-x^2},y=0,x=0;\) miền tam giác giới hạn bởi các đường \(y=2(1-x),y=0,x=0\) quanh trục Ox, ta có:

\(V=V_1-V_2\)

Ta có: \(V_1=\pi \int_{0}^{1}\left ( 2\sqrt{1-x^2} \right )^2dx= \pi \int_{0}^{1}4(1-x^2)dx\)

\(=4 \pi\int_{0}^{1}dx-4\pi \int_{0}^{1}x^2dx=4\pi x \bigg|_{0}^{1}-\frac{4}{3}\pi x^3\bigg|_{0}^{1}=\frac{8\pi }{3}\)

và: \(V_2=\pi \int _{0}^{1} \left [ 2(1-x) \right ]^2dx= 4\pi \int _{0}^{1}dx-8\pi\int _{0}^{1} x dx+4\pi \int _{0}^{1}x^2dx\)

\(=4\pi x \bigg| _{0}^{1}-4\pi x^2\bigg| _{0}^{1}+\frac{4}{3}\pi x^3\bigg| _{0}^{1} =4\pi-4\pi+\frac{4\pi }{3}=\frac{4\pi }{3}\)

Do đó: \(V=V_1-V_2=\frac{8\pi}{3}-\frac{4\pi}{3}=\frac{4\pi}{3}\).

-- Mod Toán 12