Bài tập 49 trang 176 SGK Toán 12 NC
Bài tập 49 trang 176 SGK Toán 12 NC
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
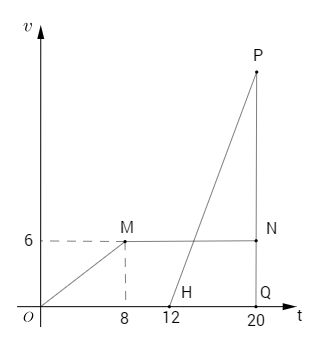
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát. Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = v.t) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = \frac{1}{2}(20 + 12).6 = 96\)
Vậy lúc gặp B, A đi được 96m.
Đồ thị vận tốc của B là đường thẳng HP. Vì B xuất phát cùng vị trí với A nên B cũng đi được 96m. Quãng đường B đi được bằng diện tích tam giác HPQ.
Ta có:
\(\begin{array}{l}
{S_{HPQ}} = \frac{1}{2}.PQ.HQ\\
\Rightarrow 96 = \frac{1}{2}PQ.8 \Rightarrow PQ = 24.
\end{array}\)
Vậy vận tốc của B tại thời điểm gặp A là 24m/s.
-- Mod Toán 12
Copyright © 2021 HOCTAP247
