Bài tập 64 trang 178 SGK Toán 12 NC
Bài tập 64 trang 178 SGK Toán 12 NC
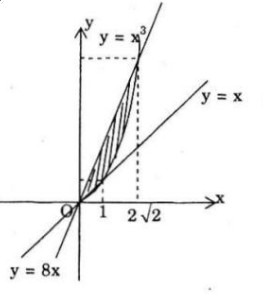
Diện tích hình phẳng nằm trong góc phần tư thứ nhất được giới hạn bới hai đường thẳng \(y = 8x,y = x\) và đồ thị hàm số \(y = {x^3}\) là:
(A) 12
(B) 15,75
(C) 6,75
(D) 4
\(\begin{array}{l}
{x^3} = 8x \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2\sqrt 2 \\
x = - 2\sqrt 2 (l)
\end{array} \right.\\
{x^3} = x \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 1\\
x = - 1(l)
\end{array} \right.
\end{array}\)
\(\begin{array}{l}
S = \int\limits_0^{2\sqrt 2 } {\left( {8x - {x^3}} \right)dx - \int\limits_0^1 {\left( {x - {x^3}} \right)dx} } \\
= \left. {\left( {4{x^2} - \frac{{{x^4}}}{4}} \right)} \right|_0^{2\sqrt 2 } - \left. {\left( {\frac{1}{2}{x^2} - \frac{1}{4}{x^4}} \right)} \right|_0^1\\
= \left( {32 - 16} \right) - \left( {\frac{1}{2} - \frac{1}{4}} \right) = 15,75
\end{array}\)
Chọn (B).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
