Bài tập 66 trang 179 SGK Toán 12 NC

Bài tập 66 trang 179 SGK Toán 12 NC

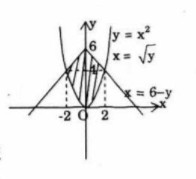
\(y = 6 - \left| x \right| = \left\{ {\begin{array}{*{20}{c}}
{6 - x,\,\,x \ge 0}\\
{6 + x{\rm{,}}\,\,x < 0}
\end{array}} \right.\)

Giao điểm của (P) với đường thẳng \(y = 6 - x\) (với x ≥ 0) là:

\(\left\{ \begin{array}{l}
{x^2} = 6 - x\\
x \ge 0
\end{array} \right. \Leftrightarrow x = 2(y = 4)\)

\(\begin{array}{l}
V = \int\limits_0^4 {\pi {{\left( {\sqrt y } \right)}^2}dy}  + \int\limits_4^6 {\pi {{\left( {6 - y} \right)}^2}dy} \\
 = \pi \int\limits_0^4 {ydy + \pi \int\limits_4^6 {{{\left( {y - 6} \right)}^2}dy} } \\
 = \pi \left. {\frac{{{y^2}}}{2}} \right|_0^4 + \pi .\frac{1}{3}\left. {{{\left( {y - 6} \right)}^3}} \right|_4^6\\
 = 8\pi  + \frac{{8\pi }}{3} = \frac{{32\pi }}{3}
\end{array}\)

Chọn (A).

-- Mod Toán 12