Bài tập 52 trang 177 SGK Toán 12 NC

Bài tập 52 trang 177 SGK Toán 12 NC

a)

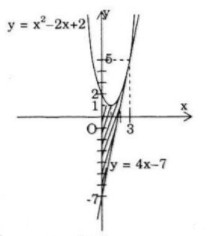
Ta có y′ = 2x − 2 ⇒ y′(3) = 4

Phương trình tiếp tuyến với parabol tại M(3;5) là:

y − 5 = 4(x − 3) ⇔ y = 4x − 7

Gọi S là diện tích cần tìm, ta có:

\(\begin{array}{*{20}{l}}
{S = \int_0^3 {({x^2} - 2x + 2 - 4x + 7)dx} }\\
\begin{array}{l}
 = \int_0^3 {({x^2} - 6x + 9)dx} \\
 = \int_0^3 {{{(x - 3)}^2}dx} 
\end{array}\\
{ = \left. {\frac{1}{3}{{\left( {x - 3} \right)}^3}} \right|_0^3 = 9}
\end{array}\)

b)

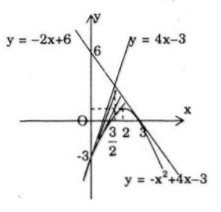
Ta có y′ = −2x + 4 ⇒ y′(0) = 4; y′(3) = −2

Phương trình tiếp tuyến tại A(0; 3) là: y + 3 = 4(x − 0) ⇔ y = 4x − 3

Phương trình tiếp tuyến tại B(3; 0) là: y = −2(x − 3) ⇔ y = −2x + 6

Giao điểm của hai tiếp tuyến là C(3/2;3). 

Kí hiệu A₁ và A₂ là tam giác cong ACD Và BCD. Ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
S({A_1}) = \int_0^{\frac{3}{2}} {(4x - 3 + {x^2} - 4x + 3)dx} \\
 = \int_0^{\frac{3}{2}} {{x^2}dx}  = \left. {\frac{{{x^3}}}{3}} \right|_0^{\frac{3}{2}} = \frac{9}{8}
\end{array}\\
\begin{array}{l}
S({A_2}) = \int_{\frac{3}{2}}^3 {( - 2x + 6 + {x^2} - 4x + 3)dx} \\
 = \int_{\frac{3}{2}}^3 {{{(x - 3)}^2}dx}  = \left. {\frac{1}{3}{{(x - 3)}^3}} \right|_{\frac{3}{2}}^3 = \frac{9}{8}
\end{array}
\end{array}\)

Vậy \(S = S({A_1}) + S({A_2}) = \frac{9}{8} + \frac{9}{8} = \frac{9}{4}\)

-- Mod Toán 12