Bài tập 3 trang 121 SGK Giải tích 12

Bài tập 3 trang 121 SGK Giải tích 12

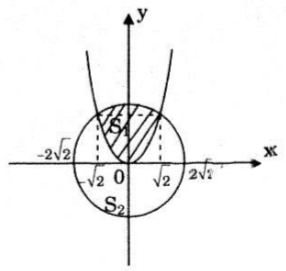
Từ hình vẽ ta có:    

\(S_1=2 \int_{0}^{2} \left [ \sqrt{8-x^2}-\frac{x^2}{2} \right ] dx\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}- \int_{0}^{2} x^2 dx\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{x^3}{3}\Bigg |^2_0\)

\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{8}{3}\)

Đặt \(x=2\sqrt{2}sint\Rightarrow dx=2\sqrt{2}costdt\)

Khi x = 0 thì  t = 0; khi x = 2 thì \(t=\frac{\pi }{4}\)

\(\Rightarrow 2\int_{0}^{2}\sqrt{8-x^2}dx=4\sqrt{2} \int_{0}^{\frac{\pi }{4}}\sqrt{8-8sin^2t}.cost dt\)

\(=16 \int_{0}^{\frac{\pi }{4}}cos^2t dt=8 \int_{0}^{\frac{\pi }{4}}(1+cos2t)dt=2\pi+4\)

\(\Rightarrow S_1=2\pi+4-\frac{8}{3}=\frac{6\pi+4}{3}\)

Gọi S là diện tích hình tròn tâm O bán kính \(R=2\sqrt{2}\) ta có \(S=8\pi .\)

Từ đó \(\Rightarrow S_2=S-S_1=8\pi-\frac{6\pi+4}{3}= \frac{18 \pi-4}{3}\)

Vậy \(\frac{S_2}{S_1}=\frac{18\pi -4}{6\pi+4}=\frac{9\pi-2}{3\pi+2}\)

-- Mod Toán 12

Video hướng dẫn giải bài 3 SGK