Bài tập 45 trang 176 SGK Toán 12 NC

Bài tập 45 trang 176 SGK Toán 12 NC

Ta có: 

\(\begin{array}{l}
\int\limits_0^b {(x - {x^2})dx}  = \left. {\left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)} \right|_0^b\\
 = \frac{{{b^2}}}{2} - \frac{{{b^3}}}{3}
\end{array}\)

Xét hàm số \(I\left( b \right) = \frac{{{b^2}}}{2} - \frac{{{b^3}}}{3}\) với b > 0

Ta có: 

\(\begin{array}{l}
I\prime (b) = b - {b^2}\\
I\prime (b) = 0 \Leftrightarrow b = 0;b = 1
\end{array}\)

Bảng biến thiên

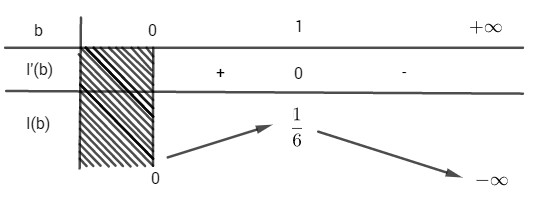
I(b) đạt giá trị lớn nhất bằng 1/6 khi b = 1

-- Mod Toán 12