Bài tập 51 trang 176 SGK Toán 12 NC

Bài tập 51 trang 176 SGK Toán 12 NC

a) Phương trình hoành độ giao điểm của hai đồ thị là:

\(\begin{array}{l}
4 - {x^2} =  - x + 2\\
 \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - 1}\\
{x = 2}
\end{array}} \right.
\end{array}\)

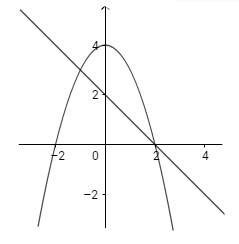
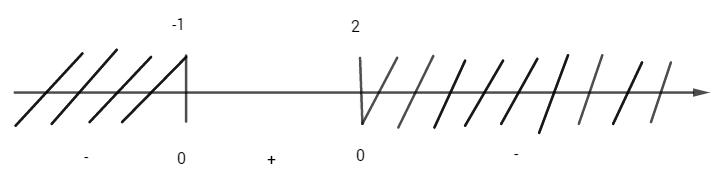
Do đó:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
S = \int_{ - 1}^2 {\mid 4 - {x^2} - ( - x + 2)\mid dx} \\
 = \int_{ - 1}^2 {| - {x^2} + x + 2\mid dx} 
\end{array}\\
\begin{array}{l}
 = \int_{ - 1}^2 {( - {x^2} + x + 2)dx} \\
 = \left. {\left( { - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} + 2x} \right)} \right|_{ - 1}^2 = \frac{9}{2}
\end{array}
\end{array}\)

b) Phương trình tung độ giao điểm của hai đồ thị là

\(\begin{array}{*{20}{l}}
\begin{array}{l}
4 - 4{y^2} = 1 - {y^4}\\
 \Leftrightarrow {y^4} - 4{y^2} + 3 = 0
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{y^2} = 1}\\
{{y^2} = 3}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{y =  \pm 1}\\
{y =  \pm \sqrt 3 \left( L \right)}
\end{array}} \right.}
\end{array}\)

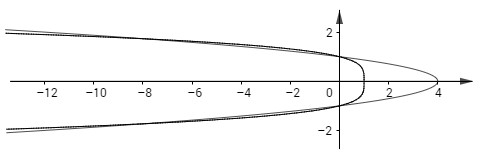
Diện tích giới hạn hai đồ thị ở phần x ≥ 0 là:

\(\begin{array}{*{20}{l}}
{S = \int_{ - 1}^1 {[4 - 4{y^2} - (1 - {y^4})]dy} }\\
{ = \int_{ - 1}^1 {({y^4} - 4{y^2} + 3)dy} }\\
\begin{array}{l}
 = \left. {\left( {\frac{{{y^5}}}{5} - \frac{4}{3}{y^3} + 3y} \right)} \right|_{ - 1}^1\\
 = 2.\frac{{28}}{{15}} = \frac{{56}}{{15}}
\end{array}
\end{array}\)

-- Mod Toán 12