Bài tập 3.32 trang 178 SBT Toán 12 NC

Bài tập 3.32 trang 178 SBT Toán 12 NC

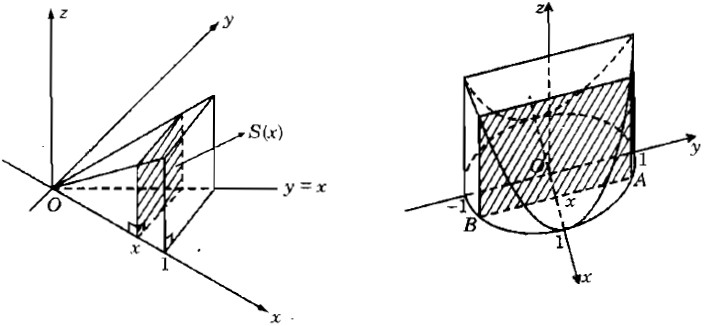
a) Với x ∈ [0;1] là hình vuông cạnh bằng x, S(x) = x².

Vậy \(V = \int \limits_0^1 S(x)dx = \int \limits_0^1 {x^2}dx = \frac{1}{3}\)

b) Thiết diện tại x∈[−1;1] là hình vuông cạnh AB, trong đó A(x; y) với \(y = \sqrt {1 - {x^2}} \).

Khi đó, \(AB = 2\sqrt {1 - {x^2}} \).

Diện tích thiết diện là: \(S(x) = 4(1 - {x^2})\)

Vậy:

\(\begin{array}{l}
V = 4\int \limits_{ - 1}^1 (1 - {x^2})dx\\
 = 8\int \limits_0^1 (1 - {x^2})dx = \frac{{16}}{3}
\end{array}\)

-- Mod Toán 12