Bài tập 59 trang 177 SGK Toán 12 NC

Bài tập 59 trang 177 SGK Toán 12 NC

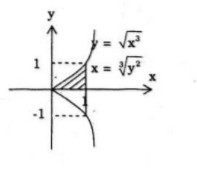
a) Ta có: \(y = \sqrt {{x^3}} (y \ge 0)\)

Thể tích cần tìm là: 

\(V = \pi \int_0^1 {{x^3}dx}  = \left. {\frac{{\pi {x^4}}}{4}} \right|_0^1 = \frac{\pi }{4}\)

b) Ta có: \(x = \sqrt[3]{{{y^2}}}\)

Thể tích cần tìm là: 

\(\begin{array}{l}
V = \pi \int_0^1 {\left( {{1^2} - \sqrt[3]{{{y^4}}}} \right)dx} \\
 = \pi \left. {\left( {y - \frac{3}{7}{y^{\frac{7}{3}}}} \right)} \right|_0^1 = \frac{\pi }{4}
\end{array}\)

-- Mod Toán 12