Bài tập 2 trang 121 SGK Giải tích 12

Bài tập 2 trang 121 SGK Giải tích 12

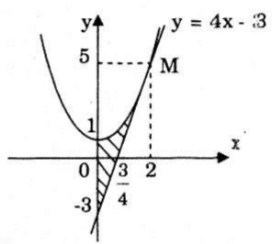
Ta lập phương trình tiếp tuyến với \(y=x^2+1\) tại M ta có \(y'=2x\Rightarrow y'(2)=4.\) Do đó phương trình tiếp tuyến với \(y=x^2+1\) tại M(2;5) có phương trình là: \(y=4x-3\)

Vậy diện tích cần tìm là:

\(S=\int_{0}^{2}|x^{2}+1 -(4x+3)|dx =\int_{0}^{2}(x^{2}-4x+4)dx\)

\(=\left ( \frac{1}{3}x^3-2x^2+4x \right ) \Bigg|^2_0 =\frac{8}{3} -8 +8=\frac{8}{3}.\) (đvdt)

-- Mod Toán 12

Video hướng dẫn giải bài 2 SGK