Bài tập 67 trang 179 SGK Toán 12 NC
Bài tập 67 trang 179 SGK Toán 12 NC
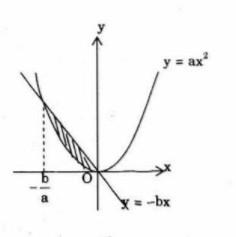
Cho a, b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai được giới hạn bởi parabol y = ax2 và đường thẳng y = −bx. Biết rằng thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc vào giá trị của a và b. Khi đó a và b thỏa mãn điều kiện sau:
(A) \({b^4} = 2{a^5}\)
(B) \({b^3} = 2{a^5}\)
(C) \({b^5} = 2{a^3}\)
(D) \({b^4} = 2{a^2}\)
\(a{x^2} = - bx \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 0}\\
{x = - \frac{b}{a}}
\end{array}} \right.\)
\(\begin{array}{l}
V = \pi \int \limits_{ - \frac{b}{a}}^0 {\left( { - bx} \right)^2}dx - \pi \int \limits_{ - \frac{b}{a}}^0 {\left( {a{x^2}} \right)^2}dx\\
= \pi \int\limits_{ - \frac{b}{a}}^0 {\left( {{b^2}{x^2} - {a^2}{x^4}} \right)dx} \\
= \pi \left. {\left( {\frac{{{b^2}{x^3}}}{3} - \frac{{{a^2}{x^5}}}{5}} \right)} \right|_{ - \frac{b}{a}}^0\\
= - \pi \left( { - \frac{{{b^5}}}{{3{a^3}}} + \frac{{{b^5}}}{{5{a^3}}}} \right) = \frac{{2\pi {b^5}}}{{15{a^3}}}
\end{array}\)
Vì \(\frac{{{b^5}}}{{{a^3}}}\) là hằng số nên ta phải chọn (C).
Khi đó \(V = \frac{{4\pi }}{{15}}.\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
