Bài tập 55 trang 221 SGK Toán 11 NC
Chương 5: Đạo Hàm
Bài tập 1 trang 156 SGK Đại số & Giải tích 11
Bài tập 2 trang 156 SGK Đại số & Giải tích 11
Bài tập 3 trang 156 SGK Đại số & Giải tích 11
Bài tập 4 trang 156 SGK Đại số & Giải tích 11
Bài tập 5 trang 156 SGK Đại số & Giải tích 11
Bài tập 6 trang 156 SGK Đại số & Giải tích 11
Bài tập 1 trang 162 SGK Đại số & Giải tích 11
Bài tập 2 trang 162 SGK Đại số & Giải tích 11
Bài tập 3 trang 163 SGK Đại số & Giải tích 11
Bài tập 4 trang 163 SGK Đại số & Giải tích 11
Bài tập 5 trang 163 SGK Đại số & Giải tích 11
Bài tập 1 trang 168 SGK Đại số & Giải tích 11
Bài tập 2 trang 168 SGK Đại số & Giải tích 11
Bài tập 3 trang 169 SGK Đại số & Giải tích 11
Bài tập 4 trang 169 SGK Đại số & Giải tích 11
Bài tập 5 trang 169 SGK Đại số & Giải tích 11
Bài tập 6 trang 169 SGK Đại số & Giải tích 11
Bài tập 7 trang 169 SGK Đại số & Giải tích 11
Bài tập 8 trang 169 SGK Đại số & Giải tích 11
Bài tập 1 trang 171 SGK Đại số & Giải tích 11
Bài tập 2 trang 171 SGK Đại số & Giải tích 11
Bài tập 7 trang 157 SGK Đại số & Giải tích 11
Bài tập 1 trang 178 SGK Đại số & Giải tích 11
Bài tập 2 trang 178 SGK Đại số & Giải tích 11
Bài tập 3 trang 178 SGK Đại số & Giải tích 11
Bài tập 4 trang 178 SGK Đại số & Giải tích 11
Bài tập 5 trang 178 SGK Đại số & Giải tích 11
Bài tập 6 trang 178 SGK Đại số & Giải tích 11
Bài tập 7 trang 178 SGK Đại số & Giải tích 11
Bài tập 8 trang 178 SGK Đại số & Giải tích 11
Bài tập 9 trang 178 SGK Đại số & Giải tích 11
Bài tập 10 trang 178 SGK Đại số & Giải tích 11
Bài tập 11 trang 178 SGK Đại số & Giải tích 11
Bài tập 12 trang 178 SGK Đại số & Giải tích 11
Bài tập 13 trang 178 SGK Đại số & Giải tích 11
Bài tập 14 trang 178 SGK Đại số & Giải tích 11
Bài tập 15 trang 178 SGK Đại số & Giải tích 11
Bài tập 16 trang 178 SGK Đại số & Giải tích 11
Bài tập 17 trang 178 SGK Đại số & Giải tích 11
Bài tập 18 trang 178 SGK Đại số & Giải tích 11
Bài tập 1 trang 178 SGK Đại số & Giải tích 11
Bài tập 2 trang 179 SGK Đại số & Giải tích 11
Bài tập 3 trang 179 SGK Đại số & Giải tích 11
Bài tập 4 trang 179 SGK Đại số & Giải tích 11
Bài tập 5 trang 179 SGK Đại số & Giải tích 11
Bài tập 6 trang 179 SGK Đại số & Giải tích 11
Bài tập 7 trang 179 SGK Đại số & Giải tích 11
Bài tập 8 trang 180 SGK Đại số & Giải tích 11
Bài tập 9 trang 180 SGK Đại số & Giải tích 11
Bài tập 10 trang 180 SGK Đại số & Giải tích 11
Bài tập 11 trang 180 SGK Đại số & Giải tích 11
Bài tập 12 trang 180 SGK Đại số & Giải tích 11
Bài tập 13 trang 180 SGK Đại số & Giải tích 11
Bài tập 14 trang 181 SGK Đại số & Giải tích 11
Bài tập 15 trang 181 SGK Đại số & Giải tích 11
Bài tập 16 trang 181 SGK Đại số & Giải tích 11
Bài tập 17 trang 181 SGK Đại số & Giải tích 11
Bài tập 18 trang 181 SGK Đại số & Giải tích 11
Bài tập 19 trang 181 SGK Đại số & Giải tích 11
Bài tập 20 trang 181 SGK Đại số & Giải tích 11
Bài tập 1 trang 176 SGK Đại số & Giải tích 11
Bài tập 2 trang 176 SGK Đại số & Giải tích 11
Bài tập 3 trang 176 SGK Đại số & Giải tích 11
Bài tập 4 trang 176 SGK Đại số & Giải tích 11
Bài tập 5 trang 176 SGK Đại số & Giải tích 11
Bài tập 6 trang 176 SGK Đại số & Giải tích 11
Bài tập 7 trang 176 SGK Đại số & Giải tích 11
Bài tập 8 trang 177 SGK Đại số & Giải tích 11
Bài tập 9 trang 177 SGK Đại số & Giải tích 11
Bài tập 10 trang 177 SGK Đại số & Giải tích 11
Bài tập 11 trang 177 SGK Đại số & Giải tích 11
Bài tập 12 trang 177 SGK Đại số & Giải tích 11
Bài tập 13 trang 177 SGK Đại số & Giải tích 11
Bài tập 1 trang 174 SGK Đại số & Giải tích 11
Bài tập 2 trang 174 SGK Đại số & Giải tích 11
Bài tập 5.66 trang 209 SBT Toán 11
Bài tập 5.67 trang 209 SBT Toán 11
Bài tập 5.68 trang 209 SBT Toán 11
Bài tập 5.69 trang 209 SBT Toán 11
Bài tập 5.70 trang 209 SBT Toán 11
Bài tập 5.71 trang 209 SBT Toán 11
Bài tập 5.72 trang 209 SBT Toán 11
Bài tập 5.73 trang 209 SBT Toán 11
Bài tập 5.74 trang 210 SBT Toán 11
Bài tập 5.75 trang 210 SBT Toán 11
Bài tập 5.76 trang 210 SBT Toán 11
Bài tập 5.77 trang 210 SBT Toán 11
Bài tập 5.78 trang 210 SBT Toán 11
Bài tập 5.79 trang 210 SBT Toán 11
Bài tập 5.80 trang 211 SBT Toán 11
Bài tập 5.81 trang 211 SBT Toán 11
Bài tập 5.12 trang 202 SBT Toán 11
Bài tập 5.13 trang 202 SBT Toán 11
Bài tập 5.14 trang 202 SBT Toán 11
Bài tập 5.15 trang 202 SBT Toán 11
Bài tập 5.16 trang 202 SBT Toán 11
Bài tập 5.17 trang 202 SBT Toán 11
Bài tập 5.18 trang 202 SBT Toán 11
Bài tập 5.19 trang 202 SBT Toán 11
Bài tập 5.20 trang 202 SBT Toán 11
Bài tập 5.21 trang 203 SBT Toán 11
Bài tập 5.22 trang 203 SBT Toán 11
Bài tập 5.23 trang 203 SBT Toán 11
Bài tập 5.24 trang 203 SBT Toán 11
Bài tập 5.25 trang 203 SBT Toán 11
Bài tập 5.26 trang 203 SBT Toán 11
Bài tập 5.27 trang 203 SBT Toán 11
Bài tập 5.28 trang 203 SBT Toán 11
Bài tập 5.29 trang 203 SBT Toán 11
Bài tập 5.30 trang 203 SBT Toán 11
Bài tập 5.31 trang 204 SBT Toán 11
Bài tập 5.32 trang 204 SBT Toán 11
Bài tập 5.33 trang 204 SBT Toán 11
Bài tập 5.34 trang 204 SBT Toán 11
Bài tập 5.35 trang 204 SBT Toán 11
Bài tập 5.36 trang 204 SBT Toán 11
Bài tập 5.37 trang 205 SBT Toán 11
Bài tập 5.38 trang 205 SBT Toán 11
Bài tập 5.39 trang 205 SBT Toán 11
Bài tập 5.1 trang 198 SBT Toán 11
Bài tập 5.2 trang 198 SBT Toán 11
Bài tập 5.3 trang 198 SBT Toán 11
Bài tập 5.4 trang 198 SBT Toán 11
Bài tập 5.5 trang 198 SBT Toán 11
Bài tập 5.6 trang 198 SBT Toán 11
Bài tập 5.7 trang 199 SBT Toán 11
Bài tập 5.8 trang 199 SBT Toán 11
Bài tập 5.9 trang 199 SBT Toán 11
Bài tập 5.10 trang 199 SBT Toán 11
Bài tập 5.11 trang 199 SBT Toán 11
Bài tập 1 trang 192 SGK Toán 11 NC
Bài tập 2 trang 192 SGK Toán 11 NC
Bài tập 3 trang 192 SGK Toán 11 NC
Bài tập 4 trang 192 SGK Toán 11 NC
Bài tập 5 trang 192 SGK Toán 11 NC
Bài tập 6 trang 192 SGK Toán 11 NC
Bài tập trang 192 SGK Toán 11 NC
Bài tập 8 trang 192 SGK Toán 11 NC
Bài tập 9 trang 192 SGK Toán 11 NC
Bài tập 10 trang 195 SGK Toán 11 NC
Bài tập 11 trang 195 SGK Toán 11 NC
Bài tập 12 trang 195 SGK Toán 11 NC
Bài tập 13 trang 195 SGK Toán 11 NC
Bài tập 14 trang 195 SGK Toán 11 NC
Bài tập 15 trang 195 SGK Toán 11 NC
Bài tập 16 trang 204 SGK Toán 11 NC
Bài tập 17 trang 204 SGK Toán 11 NC
Bài tập 18 trang 204 SGK Toán 11 NC
Bài tập 19 trang 204 SGK Toán 11 NC
Bài tập 20 trang 204 SGK Toán 11 NC
Bài tập 21 trang 204 SGK Toán 11 NC
Bài tập 22 trang 205 SGK Toán 11 NC
Bài tập 23 trang 205 SGK Toán 11 NC
Bài tập 24 trang 205 SGK Toán 11 NC
Bài tập 25 trang 205 SGK Toán 11 NC
Bài tập 28 trang 211 SGK Toán 11 NC
Bài tập 29 trang 211 SGK Toán 11 NC
Bài tập 30 trang 211 SGK Toán 11 NC
Bài tập 31 trang 212 SGK Toán 11 NC
Bài tập 32 trang 212 SGK Toán 11 NC
Bài tập 33 trang 212 SGK Toán 11 NC
Bài tập 34 trang 212 SGK Toán 11 NC
Bài tập 35 trang 212 SGK Toán 11 NC
Bài tập 36 trang 212 SGK Toán 11 NC
Bài tập 37 trang 212 SGK Toán 11 NC
Bài tập 38 trang 213 SGK Toán 11 NC
Bài tập 39 trang 215 SGK Toán 11 NC
Bài tập 40 trang 216 SGK Toán 11 NC
Bài tập 41 trang 216 SGK Toán 11 NC
Bài tập 42 trang 216 SGK Toán 11 NC
Bài tập 43 trang 216 SGK Toán 11 NC
Bài tập 43 trang 216 SGK Toán 11 NC
Bài tập 44 trang 216 SGK Toán 11 NC
Bài tập 45 trang 219 SGK Toán 11 NC
Bài tập 46 trang 219 SGK Toán 11 NC
Bài tập 47 trang 219 SGK Toán 11 NC
Bài tập 48 trang 219 SGK Toán 11 NC
Bài tập 49 trang 220 SGK Toán 11 NC
Bài tập 50 trang 221 SGK Toán 11 NC
Bài tập 51 trang 221 SGK Toán 11 NC
Bài tập 52 trang 221 SGK Toán 11 NC
Bài tập 53 trang 221 SGK Toán 11 NC
Bài tập 54 trang 221 SGK Toán 11 NC
Bài tập 55 trang 221 SGK Toán 11 NC
Bài tập 56 trang 221 SGK Toán 11 NC
Bài tập 57 trang 222 SGK Toán 11 NC
Bài tập 58 trang 222 SGK Toán 11 NC
Bài tập 59 trang 222 SGK Toán 11 NC
Bài tập 60 trang 222 SGK Toán 11 NC
Bài tập 61 trang 222 SGK Toán 11 NC
Bài tập 62 trang 223 SGK Toán 11 NC
Bài tập 63 trang 223 SGK Toán 11 NC
Bài tập 1 trang 223 SGK Toán 11 NC
Bài tập 2 trang 223 SGK Toán 11 NC
Bài tập 3 trang 223 SGK Toán 11 NC
Bài tập 4 trang 223 SGK Toán 11 NC
Bài tập 5 trang 224 SGK Toán 11 NC
Bài tập 6 trang 224 SGK Toán 11 NC
Bài tập 7 trang 224 SGK Toán 11 NC
Bài tập 8 trang 224 SGK Toán 11 NC
Bài tập 9 trang 224 SGK Toán 11 NC
Bài tập 10 trang 224 SGK Toán 11 NC
Bài tập 11 trang 225 SGK Toán 11 NC
Bài tập 12 trang 225 SGK Toán 11 NC
Bài tập 13 trang 225 SGK Toán 11 NC
Bài tập 14 trang 225 SGK Toán 11 NC
Bài tập 15 trang 225 SGK Toán 11 NC
Bài tập 16 trang 226 SGK Toán 11 NC
Bài tập 17 trang 226 SGK Toán 11 NC
Bài tập 18 trang 226 SGK Toán 11 NC
Bài tập 19 trang 226 SGK Toán 11 NC
Bài tập 20 trang 226 SGK Toán 11 NC
Bài tập 21 trang 226 SGK Toán 11 NC
Bài tập 22 trang 227 SGK Toán 11 NC
Bài tập 23 trang 227 SGK Toán 11 NC
Bài tập 24 trang 227 SGK Toán 11 NC
Bài tập 25 trang 227 SGK Toán 11 NC
Bài tập 55 trang 221 SGK Toán 11 NC
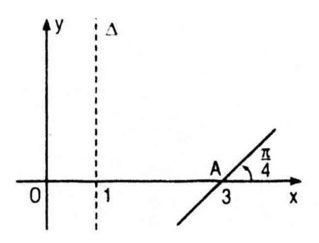
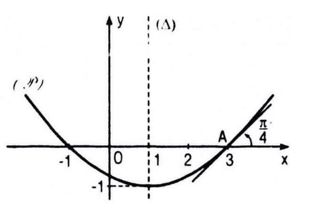
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
Đa thức phải tìm có dạng : P(x) = ax2 + bx + c (a ≠ 0)
Ta có: P′(x) = 2ax + b
Vì trục đối xứng (∆) có phương trình x = 1 nên : \(\frac{{ - b}}{{2a}} = 1\) (1)
Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là: 9a + 3b + c = 0 (2)
Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(tan\frac{\pi }{4}\) nên ta có P′(3) = 1, tức là :
6a + b = 1(3)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được:
\(\begin{array}{l}
a = \frac{1}{4}\\
b = - \frac{1}{2}\\
c = - \frac{3}{4}
\end{array}\)
Vậy \(P(x) = \frac{1}{4}{x^2} - \frac{1}{2}x - \frac{3}{4}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
