Bài tập 1 trang 178 SGK Đại số & Giải tích 11

Bài tập 1 trang 178 SGK Đại số & Giải tích 11

Câu a:

Ta có: \(cos2(x+k\pi )=cos(2x+2k\pi )=cos2x, \forall k\in \mathbb{Z}, \forall x\in \mathbb{R}\)

Sử dụng tính chất trên, ta chỉ cần vẽ đồ thị hàm số \(y=cos2x\) trên miền \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\), từ đó suy ra đồ thị hàm số \(y=cos2x\) trên \(\mathbb{R}\).

Đồ thị hàm số \(y=cos2x\) trên miền \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\).

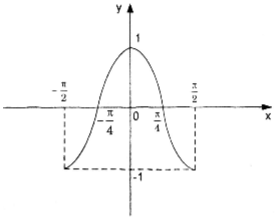
Đồ thị hàm số \(y=cos2x\) trên \(\mathbb{R}\).

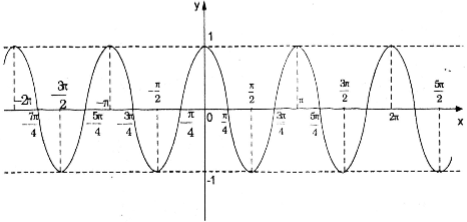
Câu b:

Ta có: \(y'=-2sin2x\Rightarrow y'\left ( \frac{\pi }{3} \right )=-2sin\frac{2\pi }{3}=-\sqrt{3}\)

Mặt khác điểm trên đồ thị (C) có hoành độ là \(\frac{\pi }{3}\) thì có tung độ \(y=cos\frac{2\pi }{3}\) hay \(y=-\frac{1}{2}\). Vì vậy phương trình tiếp tuyến tại điểm \(\left ( \frac{\pi }{3};-\frac{1}{2} \right )\) có dạng: \(y=-\sqrt{3}\left ( x-\frac{\pi }{3} \right )-\frac{1}{2}\Leftrightarrow y=- \sqrt{3}x+\frac{\sqrt{3}\pi }{3}-\frac{1}{2}\)

Câu c:

Dễ thấy \(1+cos^22x\geq 1, \forall x\in \mathbb{R}\), do đó hàm số đã cho được xác định khi và chỉ khi \(1-cos2x\geq 0\Leftrightarrow cos2x\leq 1\) được thoả mãn với mọi \(x\in \mathbb{R}\)

Vậy tập xác định của hàm số \(z=\sqrt{\frac{1-cos2x}{1+cos^22x}}\) là tập \(\mathbb{R}\).

-- Mod Toán 11