Bài tập 1.16 trang 19 SBT Hình học 12

Bài tập 1.16 trang 19 SBT Hình học 12

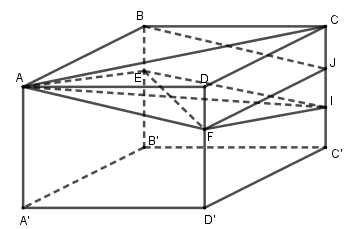
Gọi \(I = CC' \cap \left( {AEF} \right)\)

Vì \(\left\{ {\begin{array}{*{20}{l}}
{\left( {AEF} \right) \cap \left( {ABB'A'} \right) = AE}\\
{\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI}\\
{\left( {ABB'A'} \right)\parallel \left( {CDD'C'} \right)}
\end{array}} \right.\) 

Nên AE // FI.

Tương tự AF // EI nên tứ giác AEIF là hình bình hành.

Trên cạnh C lấy điểm J sao cho CJ = DF.

Dễ thấy FJ // CD // AB$,$ FI = CD = AB 

Nên ABJF là hình bình hành \( \Rightarrow AF//BJ,AF = BJ\).

Suy ra EI // BJ, EI = BJ hay EBJI là hình bình hành \( \Rightarrow BE = JI\).

Từ đó suy ra \(IJ = EB = DF = JC = \frac{c}{3}\)

Ta có \({S_{BCIE}} = \frac{1}{2}\left( {\frac{{c + 2c}}{3}} \right)b = \frac{{bc}}{2},\)

\({S_{DCIF}} = \frac{1}{2}\left( {\frac{{c + 2c}}{3}} \right)a = \frac{{ac}}{2}\)

Nên \({V_{(H)}} = {V_{A.BCIE}} + {V_{A.DCIF}} \)

\(= \frac{1}{3}.\frac{{bc}}{2}.a + \frac{1}{3}.\frac{{ac}}{2}.b = \frac{{abc}}{3}\)

Lại có:

\({V_{ABCD.A'B'C'D'}} = abc \Rightarrow {V_{(H')}} = \frac{2}{3}abc\)

\( \Rightarrow \frac{{{V_{(H)}}}}{{{V_{(H')}}}} = \frac{1}{2}\)

-- Mod Toán 12