Bài tập 27 trang 35 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 27 trang 35 SGK Hình học 12 NC
Cho một hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Thể tích của hình chóp đó là:
(A) \(\frac{{{a^3}\cot \alpha }}{{12}}\)
(B) \(\frac{{{a^3}\tan \alpha }}{{12}}\)
(C) \(\frac{{{a^2}\tan \alpha }}{{12}}\)
(D) \(\frac{{{a^3}\tan \alpha }}{4}\)
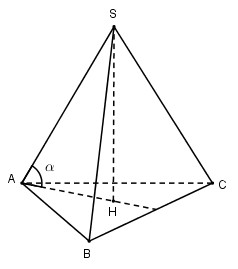
Gọi H là tâm của tam giác đều ABC thì \(SH \bot \left( {ABC} \right)\)
\(\tan \alpha = \frac{{SH}}{{AH}} \Rightarrow SH = \frac{{a\sqrt 3 }}{3}\tan \alpha \)
Thể tích hình chóp là:
\(\begin{array}{l}
V = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}\frac{{{a^2}\sqrt 3 }}{4}\frac{{a\sqrt 3 }}{3}\tan \alpha \\
= \frac{{{a^3}\tan \alpha }}{{12}}
\end{array}\)
Chọn (B).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
