Bài tập 1.33 trang 20 SBT Hình học 12

Bài tập 1.33 trang 20 SBT Hình học 12

Gọi cạnh của tứ diện đều là a thì cạnh của hình bát diện đều (H) là \(\frac{a}{2}\).

+) Tính thể tích tứ diện đều ABCD cạnh a.

Gọi E là trung điểm của BC và F là trọng tâm của tam giác ABC.

Khi đó \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)

Và \(DF = \sqrt {D{A^2} - A{F^2}}  \)

\(= \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}= \frac{{a\sqrt 6 }}{3}\)

\( \Rightarrow {V_{ABCD}} = \frac{1}{3}{S_{ABC}}.DF = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 6 }}{3} \)

\(= \frac{{{a^3}\sqrt 2 }}{{12}}\).

+) Tính thể tích khối bát diện đều cạnh \(\frac{a}{2}\).

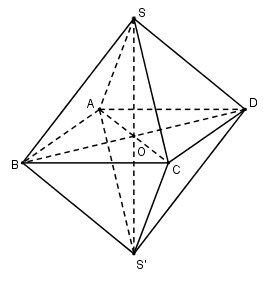
Xét bát diện đều SABCDS′ có cạnh \(\frac{a}{2}\).

Thể tích khối bát diện đều \({V_{\left( H \right)}} = 2{V_{S.ABCD}}\)

Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)

Vì ABCD là hình vuông nên \(AC = BD = \frac{{a\sqrt 2 }}{2} \)

\(\Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{4}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \)

\(\Rightarrow \Delta SOA\) vuông tại O

\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}}  \)

\(= \sqrt {{{\left( {\frac{a}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 2 }}{4}} \right)}^2}}  \)

\(= \frac{{a\sqrt 2 }}{4}\)

\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} \)

\(= \frac{1}{3}\frac{{a\sqrt 2 }}{4}.{\left( {\frac{a}{2}} \right)^2} = \frac{{{a^3}\sqrt 2 }}{{48}}\)

\( \Rightarrow {V_{\left( H \right)}} = 2.\frac{{{a^3}\sqrt 2 }}{{48}} = \frac{{{a^3}\sqrt 2 }}{{24}}\)

Vậy \(\frac{{{V_{(H)}}}}{{{V_{ABCD}}}} = \frac{1}{2}\).

-- Mod Toán 12