Bài tập 7 trang 26 SGK Hình học 12

Bài tập 7 trang 26 SGK Hình học 12

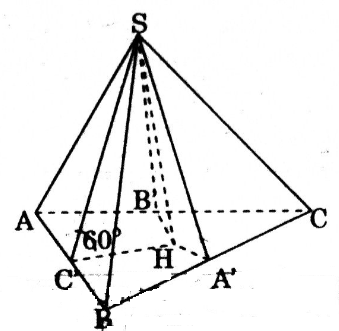
Gọi H là hình chiếu của S lên mặt phẳng (ABC). Gọi A', B', C' lần lượt là hình chiếu của H lên các cạnh BC, CA, AB. Xét các tam giác vuông: SHA', SHB', SHC' có:

\(\widehat{SA'H}=\widehat{SB'H}=\widehat{SC'H}=60^0\) (vì các góc này chính là các góc của mặt bên và mặt đáy ABC)

Từ các tam giác vuông đó dễ dàng suy ra \(SC'=SA'=SB'\) nên HA' = HB'= HC' ⇒ H là tâm đường tròn nội tiếp tam giác ABC.

Mặt khác diện tích của tam giác ABC có thể tính theo công thức:

\(S_{\Delta ABC}=\sqrt{p(p-AB)(p-AC)(p-BC)}\)

Với \(p=\frac{AB+AC+BC}{2}=\frac{5a+6a+7a}{2}=9a\)

Do đó: 

\(S_{\Delta ABC}=\sqrt{(9a-5a)(9a-6a)(9a-7a)p}\)

\(=\sqrt{216a^4}=6a^2\sqrt{6}\)

Vì \(S_{\Delta ABC}=p.r\) (r là bán kính đường tròn nội tiếp tam giác ABC)

\(\Rightarrow r=\frac{6a^2\sqrt{6}}{9a}=\frac{2a\sqrt{6}}{3}\)

Xét tam giác vuông SHA', ta có: \(tan 60^0=\frac{SH}{HA'}\Rightarrow SH=r.tan60^0\)

\(\Rightarrow SH=\frac{2a\sqrt{6}}{3}.\sqrt{3}=2\sqrt{2}a\)

Do đó thể tích của khối chóp S.ABC là:

\(V_{S.ABC}=\frac{1}{3}S._{\Delta ABC}.SH\)

\(=\frac{1}{3}.6.a^2\sqrt{6}. 2\sqrt{2}a=8\sqrt{3}a^3\)

-- Mod Toán 12