Bài tập 30 trang 36 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 30 trang 36 SGK Hình học 12 NC
Một khối chóp tam giác có cạnh đáy bằn 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 600. Thể tích của khối chóp đó là:
(A) \(16\sqrt 3 \)
(B) \(8\sqrt 3 \)
(C) \(16\frac{{\sqrt 2 }}{3}\)
(D) \(16\pi \)
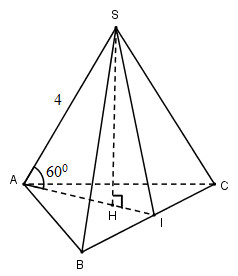
Kẻ đường cao SH của hình chóp S.ABC
\(SH = SA.\sin {60^0} = 4.\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \)
Diện tích tam giác ABC là:
\({S_{ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 24\)
Thể tích của khối chóp là:
\(V = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}.24.2\sqrt 3 = 16\sqrt 3 \)
Chọn (A).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
