Bài tập 6 trang 26 SGK Hình học 12
Bài tập 6 trang 26 SGK Hình học 12
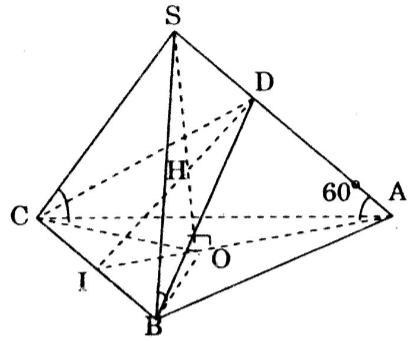
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một góc bằng 600. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA.
a) Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC
b) Tính thể tích khối chóp S.DBC
Câu a:
Ta có: AB = BC = CA = a
Gọi O là hình chiều vuông góc của (S) lên (ABC)
Khi đó ta có: \(\widehat{SBO}=\widehat{SCO}=\widehat{SAO}=60^0\)
\(\Rightarrow \Delta SOA=\Delta SOB=\Delta SOC\)
\(\Rightarrow OA=OB=OC\) hay O là tâm của tam giác đều ABC.
Trong các tam giác SOA, SOB, SOC. Ta có:
\(SA=SB=SC=2OA=2.\frac{2}{3}.\frac{a\sqrt{3}}{2}\)
\(=\frac{2a\sqrt{3}}{3}\)
\(SO=\sqrt{SB^2-OB^2}=a\)
Gọi I là trung điểm của BC, ta có: \(ID\perp SA\)
Nên \(ID. SA=SO.IA\)
\(\Rightarrow ID=\frac{a.\frac{a\sqrt{3}}{2}}{\frac{2a\sqrt{3}}{3}}= \frac{3}{4}a\)
Xét tam giác vuông IDA, ta có:
\(DA=\sqrt{IA^2-ID^2}=\frac{a\sqrt{3}}{4}\)
\(\Rightarrow SD=\frac{2a\sqrt{3}}{3}- \frac{a\sqrt{3}}{4}=\frac{5a\sqrt{3}}{12}\)
Mặt khác:
\(\frac{V_{S.ABC}}{V_{S.DBC}}=\frac{V_{S.DBC}+V_{A.BCD}}{V_{SDBC}}= 1+\frac{AD}{SD}\)
\(=1+\frac{\frac{a\sqrt{3}}{4}}{\frac{5a\sqrt{3}}{12}}=\frac{8}{5}\Rightarrow \frac{V_{S.DBC}}{V_{S.ABC}}=\frac{5}{8}\)
Câu b:
Ta có: \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4};SH = AH.\tan {60^0} = a\)
\( \Rightarrow {V_{SABC}} = \frac{1}{3}.SH.{S_{ABC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Từ kết quả câu a) ta có:
\({V_{S.DBC}} = \frac{5}{8}.{V_{S.ABC}} = \frac{5}{8}.\frac{{{a^3}\sqrt 3 }}{{12}} = \frac{{5{a^3}\sqrt 3 }}{{96}}\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
