Bài tập 1.46 trang 22 SBT Hình học 12

Bài tập 1.46 trang 22 SBT Hình học 12

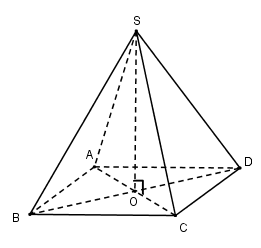
Gọi \(O = AC \cap BD\)

Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)

Ta có: 

\(AC = BD = a\sqrt 2  \)

\(\Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O

\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{a^2} - \frac{{{a^2}}}{2}}  \)

\(= \frac{{a\sqrt 2 }}{2}\)

Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}\frac{{a\sqrt 2 }}{2}{a^2} \)

\(= \frac{{{a^3}\sqrt 2 }}{6}\)

Chọn B.

-- Mod Toán 12