Bài tập 10 trang 27 SGK Hình học 12
Bài tập 10 trang 27 SGK Hình học 12
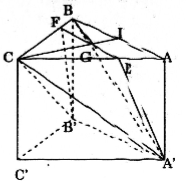
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a.
a) Tính thể tích khối tứ diện A'BB'C
b) Mặt phẳng đi qua A'B' và trọng tâm tam giác ABC cắt AC và BC lần lượt tạ E và F. Tính thể tích hình chóp C.A'B'FE.
Câu a:
Ta tính thể tích hình chóp A'.BCB'.
Gọi M là trung điểm của B'C', ta có: \(A'M\perp B'C'\) (1)
Lăng trụ ABC.A'B'C' là lăng trụ đứng nên: \(BB'\perp (A'B'C')\)
\(\Rightarrow BB'\perp A'M\)
Từ (1) và (2) suy ra \(A'M\perp (BB'C)\) hay A'M là đường cao của hình chóp A'.BCB'.
Ta có: \(A'M=\frac{a\sqrt{3}}{2};S_{BB'C}=\frac{1}{2}a^2\)
\(\Rightarrow V_{A'BB'C}=\frac{1}{3}A'M.S_{BB'C}\)
\(\Rightarrow V_{A'BB'C}=\frac{a^3\sqrt{3}}{12}\)
Câu b:
Thể tích hình chóp C.A'B'EF bằng tổng thể tích hai hình chóp:
- V1 là thể tích hình chóp đỉnh B', đáy là tam giác CEF.
- V2 là thể tích hình chóp đỉnh B', đáy là tam giác A'EC.
Do mp (ABC) // mp(A'B'C') nên dễ thấy EF // AB. Ta cũng có: \(EF=\frac{2}{3}a\)
Hình chóp B'.CEF có chiều cao BB' = a và diện tích đáy là:
\(S_{CEF}=\frac{1}{2}.\frac{2a}{3}.\frac{2}{3}.\frac{a\sqrt{3}}{3}=\frac{a^2\sqrt{3}}{9}\)
Từ đây ta có: \(V_1=\frac{a^3\sqrt{3}}{27}\)
Do \(EC=\frac{2}{3}AC\) nên:
\(S_{A'EC}=\frac{2}{3}a.\frac{1}{2}a=\frac{a^2}{3}\)
Hình chóp B'.A'EC có chiều cao là B'I (chiều cao của \(\Delta A'B'C'\)) bằng \(\frac{a\sqrt{3}}{2}\) nên \(V_2=\frac{a^3\sqrt{3}}{18}\)
Vậy thể tích hình chóp C.A'B'FE là: \(V=V_1+V_2=\frac{5a^3\sqrt{3}}{54}\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
