Bài tập 7 trang 28 SGK Hình học 12

Bài tập 7 trang 28 SGK Hình học 12

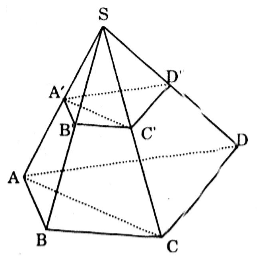
\(\frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC} =\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}\)

\(\Rightarrow V_{S.A'B'C'}=\frac{1}{8}V_{S.ABC}\)  (1)

Tương tự: \(V_{S.A'C'D'}=\frac{1}{8}V_{S.ACD}\)  (2)

Lấy (1) cộng (2) ta được:

\(V_{S.A'B'C'D'}=V_{S.A'B'C'}+V_{S.A'C'D'}\)

\(= \frac{1}{8}(V_{S.ABC}+V_{S.ACD})= \frac{1}{8}V_{S.ABCD}\)

Vậy \(\frac{V_{S.A'B'C'D'}}{V}=\frac{1}{8}\)

⇒ Chọn đáp án C

-- Mod Toán 12