Bài tập 5 trang 26 SGK Hình học 12

Bài tập 5 trang 26 SGK Hình học 12

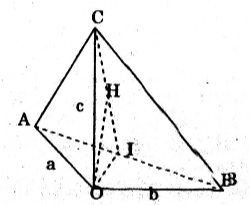
Gọi I là hình chiếu của O lên AB. Vì OC vuông góc với OA và OB nên \(OC\perp (OAB)\Rightarrow OC\perp AB\).

Từ đó ta suy ra: \(AB\perp (COI)\).

Vậy H là hình chiếu của O lên CI.

Trong tam giác vuông AOB ta có:

\(\frac{1}{OI^2}=\frac{1}{OA^2}+\frac{1}{OB^2} \ \ \ (1)\)

Trong tam giác vuông COI ta có: \(\frac{1}{OH^2}=\frac{1}{OI^2}+\frac{1}{OC^2} \ \ (2)\)

Từ (1) và (2) ta có:

\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2} + \frac{1}{OC^2} \)

\(= \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)

\(=\frac{a^2b^2+b^2c^2+c^2a^2}{a^2b^2c^2}\)

\(\Leftrightarrow OH=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}\)

Nhận xét: Ta có thể tính OH từ mối liên hệ:

\(V_{O.ABC}=\frac{1}{6}abc=\frac{1}{3}.OH.S_{\Delta ABC}\)

-- Mod Toán 12