Bài tập 18 trang 33 SGK Hình học 12 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 18 trang 33 SGK Hình học 12 NC
Đáy của một hình hộp đứng là hình thoi cạnh a, góc nhọn 600. Đường chéo lớn của đáy bằng đường chéo nhỏ của hình hộp. Khi đó thể tích của hình hộp là:
(A) \({a^3}\)
(B) \({a^3}\sqrt 3 \)
(C) \(\frac{{{a^3}\sqrt 3 }}{2}\)
(D) \(\frac{{{a^3}\sqrt 3 }}{6}\)
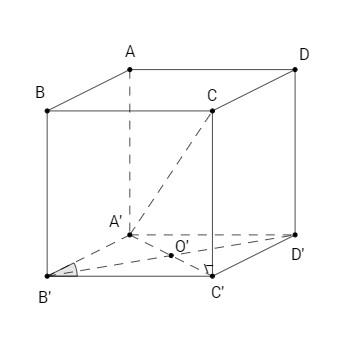
Tam giác A’B’C’ là tam giác đều cạnh a
Ta có:
\(\begin{array}{l}
A'C' = a\\
B'D' = 2B'O' = a\sqrt 3 = A'C\\
\Rightarrow CC' = \sqrt {A'{C^2} - A'{C^{\prime 2}}} \\
= \sqrt {3{a^2} - {a^2}} = a\sqrt 2
\end{array}\)
Diện tích đáy:
\({S_{A'B'C'D'}} = \frac{1}{2}A'C'.B'D' = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích khối hộp:
\(V = S.h = \frac{{{a^2}\sqrt 3 }}{2}.a\sqrt 2 = \frac{{{a^3}\sqrt 6 }}{2}\)
Chọn (D).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
