Bài tập 28 trang 35 SGK Hình học 12 NC

Bài tập 28 trang 35 SGK Hình học 12 NC

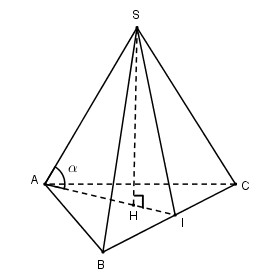
Gọi H là tâm của tam giác đều ABC cạnh a.

\(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = \alpha \)

I là trung điểm của BC

\(AH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)  

Trong tam giác vuông AHS có:

\(\begin{array}{l}
\cos \alpha  = \frac{{AH}}{{SA}} \Rightarrow b\cos \alpha  = \frac{{a\sqrt 3 }}{3}\\
 \Rightarrow a = b\sqrt 3 \cos \alpha 
\end{array}\)

Diện tích tam giác ABC: 

\({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{4}{b^2}{\cos ^2}\alpha \)

Mặt khác \(SH = SA\sin \alpha  = b\sin \alpha \)

Thể tích hình chóp là:

\(V = \frac{1}{3}{S_{ABC}}.SH = \frac{{\sqrt 3 }}{4}{b^3}{\cos ^2}\alpha \sin \alpha \)

Chọn (B).

-- Mod Toán 12