Bài tập 12 trang 27 SGK Hình học 12
Bài tập 12 trang 27 SGK Hình học 12
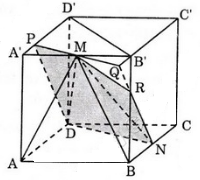
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm A'B', N là trung điểm BC.
a) Tính thể tích khối tứ diện BC.
b) Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A, (H) là khối đa diện còn lại. Tính tỉ số \(\frac{V_{(H)}}{V_{(H')}}\)
Câu a:
Ta tính thể tích hình chóp M.ADN. Hình chóp này có chiều cao bằng a và diện tích AND bằng \(\frac{a^2}{2}\)
\(V_{ADMN}=\frac{1}{3}a.\frac{a^2}{2}=\frac{a^3}{6}\)
Câu b:
Trước hết, ta dựng thiết diện của hình lập phương khi cắt bởi mp(DMN).
Do (ABCD) // (A'B'C'D') nên (DMN) cắt (A'B'C'D') theo một giao tuyến song song với DN. Ta dựng thiết diện như sau:
- Từ M kẻ đường thẳng song song với DN, đường này cắt cạnh A'D' tại điểm P và cắt đường thẳng C'B' tại điểm Q. Trong mặt phẳng (BCC'B') thì QN cắt cạnh BB' tại điểm R; đa giác DNRMP chính là thiết diện của hình lập phương khi cắt bởi mp (DMN).
- Bây giờ ta tính thể tích khối đa diện ABNDPMR. Thể tích này có thể coi là thể tích của ba hình chóp.
V1 là thể tích hình chóp đáy ABND, đỉnh M;
V2 là thể tích hình chóp đáy AA'PD, đỉnh M;
V3 là thể tích hình chóp đáy NRB, đỉnh M
Hình chóp M.ABND, có đường cao bằng a, diện tích đáy là hình thang ABND là:
\(\frac{1}{2}\left ( \frac{a}{2}+a \right ).a=\frac{3a^2}{4}\)
Suy ra: \(V_1=\frac{1}{3}.\frac{3a^2}{4}.a\Rightarrow V=\frac{a^3}{4}\)
Dễ thấy \(A'P=\frac{a}{4}\). Hình chóp M.AA'PD có chiều cao \(\frac{a}{2}\) và diện tích hình thang AA'PD là: \(\frac{1}{2}\left ( \frac{a}{4}+a \right )a=\frac{5a^2}{8}\)
Suy ra: \(V_2=\frac{1}{3}.\frac{a}{2}.\frac{5a^2}{8}\Rightarrow V_2= \frac{5a^2}{48}\)
Dễ thấy \(BR=\frac{2}{3}a\). Diện tích tam giác NRB là: \(\frac{1}{2}.\frac{2}{3}a.\frac{a}{2}=\frac{a^2}{6}\)
Hình chóp M.NRB có chiều cao \(\frac{a}{2}\) và diện tích đáy \(\frac{a^2}{6}\) nên:
\(V_2=\frac{1}{3}.\frac{a}{2}.\frac{a^2}{6}\Rightarrow V_3=\frac{a^3}{36}\)
\(V_{ABNDPMR}=V_1+V_2+V_3\)
\(= \frac{5a^3}{48}+\frac{a^3}{4}+\frac{a^3}{36}=\frac{55a^3}{144}\)
Thể tích phần còn lại là: \(\frac{144a^3}{144}-\frac{55a^3}{144}=\frac{89a^3}{144}\)
Từ đây suy ra tỉ số cần tìm là: \(\frac{55}{89}\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
