Bài tập 20 trang 34 SGK Hình học 12 NC
Bài tập 20 trang 34 SGK Hình học 12 NC
Cho một hình hộp với sáu mặt đều là hình thoi cạnh a, góc nhọn bằng 600. Khi đó thể tích của hình hộp là:
(A) \(\frac{{{a^3}\sqrt 3 }}{3}\)
(B) \(\frac{{{a^3}\sqrt 2 }}{2}\)
(C) \(\frac{{{a^3}\sqrt 2 }}{3}\)
(D) \(\frac{{{a^3}\sqrt 3 }}{2}\)
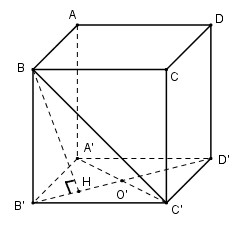
\({\rm{\Delta }}A'B'C'\) đều cạnh a
\(A'C' = a;B'D' = 2B'O' = a\sqrt 3 \)
Tương tự BA′ = BC′ = BB′ = a nên hình chiếu H của B trên mp(A’B’C’D’) là tâm của tam giác đều A′B′C′.
Ta có:
\(\begin{array}{l}
BH = \sqrt {B{B^{\prime 2}} - B'{H^2}} \\
= \sqrt {{a^2} - \frac{{{a^2}}}{3}} = \frac{{a\sqrt 6 }}{3}
\end{array}\)
\(\begin{array}{l}
{S_{A'B'C'D'}} = \frac{1}{2}A'C'.B'D'\\
= \frac{1}{2}a.a\sqrt 3 = \frac{{{a^2}\sqrt 3 }}{2}
\end{array}\)
Thể tích khối hộp là:
\(V = B.h = \frac{{{a^2}\sqrt 3 }}{2}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 2 }}{2}\)
Chọn (B).
-- Mod Toán 12
Copyright © 2021 HOCTAP247
