Bài tập 42 trang 209 SGK Toán 12 NC
Bài tập 42 trang 209 SGK Toán 12 NC
a) Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(\tan a = \frac{1}{2},\tan b = \frac{1}{3}\) với \(a,b \in \left( {0;\frac{\pi }{2}} \right)\) thì \(a + b = \frac{\pi }{4}\)
b) Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(\tan a = \frac{1}{2},\tan b = \frac{1}{5}\), \(\tan c = \frac{1}{8}\) với \(a,b,c \in \left( {0;\frac{\pi }{2}} \right)\) thì \(a + b + c= \frac{\pi }{4}\)
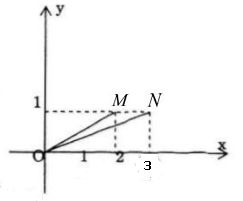
a) Biểu diễn hình học 2+i, 3+i theo thứ tự bới M và N trong mặt phẳng phức, ta có:
\(\begin{array}{*{20}{l}}
{\tan (Ox,OM) = \frac{1}{2} = \tan a}\\
{\tan (Ox,ON) = \frac{1}{3} = \tan b}
\end{array}\)
Xét \(z.z' = (2 + i).(3 + i) = 5(1 + i)\)
\( = 5\sqrt 2 \left( {\cos \frac{\pi }{4} + i\sin \frac{\pi }{4}} \right)\)
Số zz′ có acgumen là π/4, suy ra \(a + b = \frac{\pi }{4}\)
b) z1 = 2 + i có một acgumen là a với tan a = 1/2
z2 = 5 + i có một acgumen là b với tan b = 1/5
z3 = 8 + i có một acgumen là c với tan c = 1/8
Xét
\(\begin{array}{l}
z = {z_1}.{z_2}.{z_3} = \left( {2 + i} \right)\left( {5 + i} \right)\left( {8 + i} \right)\\
= 65\left( {1 + i} \right)
\end{array}\)
\(\begin{array}{l}
= 65\sqrt 2 \left( {\frac{{\sqrt 2 }}{2} + i\frac{{\sqrt 2 }}{2}} \right)\\
= 65\sqrt 2 \left( {\cos \frac{\pi }{4} + i\sin \frac{\pi }{4}} \right)
\end{array}\)
Số z có acgumen là π/4, suy ra:
\(a + b + c = \frac{\pi }{4}\)
-- Mod Toán 12
Copyright © 2021 HOCTAP247
