Bài tập 5.9 trang 220 SBT Toán 12

Bài tập 5.9 trang 220 SBT Toán 12

a) \(y = \frac{1}{3}{x^3} + {x^2} - 3x + 4\frac{1}{2}\)

+) Tập xác định: D = R

+) Sự biến thiên: y’ = x2 + 2x – 3

\(y\prime  = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x =  - 3
\end{array} \right.\)

Bảng biến thiên:

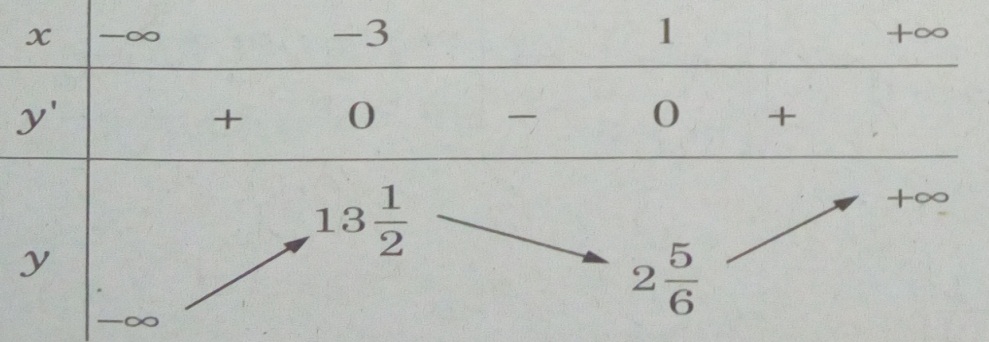
Hàm số đồng biến trên các khoảng (-∞; -3) và (1; +∞), nghịch biến trên khoảng (-3; 1).

Hàm số đạt cực đại tại 

\(x =  - 3;{y_{CD}} = 13\frac{1}{2};{y_{CT}} = 2\frac{5}{6}\) khi x = 1

Đồ thị cắt trục tung tại điểm \((0;4\frac{1}{2})\) và có dạng như hình dưới đây.

\(y'' = 2x + 2;y'' = 0 \Leftrightarrow x =  - 1\)

$\mathrm{}$Vậy là tâm đối xứng của đồ thị.

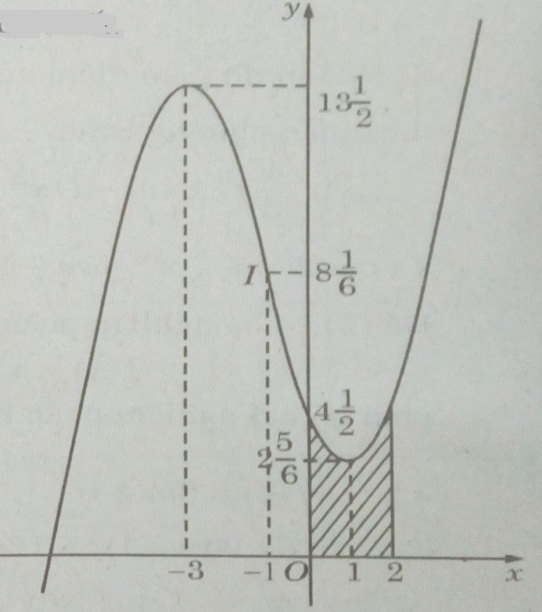
b) Tiếp tuyến với (C) đi qua \(A(0;4\frac{1}{2})\) có phương trình là: \(y = f'(0)x + 4\frac{1}{2}\), trong đó \(f(x) = \frac{1}{3}{x^3} + {x^2} - 3x + 4\frac{1}{2}\)

Ta có f ’(0) = -3.

Vậy phương trình tiếp tuyến là \(y =  - 3x + 4\frac{1}{2}\)

c) \(S = \int \limits_0^2 (\frac{1}{3}{x^3} + {x^2} - 3x + 4\frac{1}{2})dx = 7\)

(đơn vị diện tích).

d) Hoành độ giao điểm của đường thẳng \(y =  - 3x + 4\frac{1}{2}\) với đồ thị của (1) thỏa mãn phương trình

\(\begin{array}{l}
\frac{1}{3}{x^3} - (m - 1){x^2} + (m - 3)x + 4\frac{1}{2}\\
 =  - 3x + 4\frac{1}{2}
\end{array}\)

Ta có 

\((2) \Leftrightarrow \frac{1}{3}{x^3} - (m - 1){x^2} + mx = 0\)

\( \Leftrightarrow x[{x^2} - 3(m - 1)x + 3m] = 0\)

Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x2– 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
f(0) = 3m \ne 0\\
\Delta  = 9{(m - 1)^2} - 12m > 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
\left[ \begin{array}{l}
m < \frac{1}{3},m \ne 0\\
m > 3
\end{array} \right.
\end{array} \right.
\end{array}\)

-- Mod Toán 12