Bài tập 7 trang 146 SGK Giải tích 12

Bài tập 7 trang 146 SGK Giải tích 12

Phương pháp:

Câu a: Vận dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức bậc nhất trên bậc nhất.

Câu b: Lập phương trình hoành độ giao điểm để tìm tọa độ giao điểm. 

Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại tiếp điểm M(x0,y0) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng:

\(y-y_0=f'(x_0)(x-x_0)\)

Câu c: Ứng dụng tích phân tính thể tích khối tròn xoay.

Lời giải:

Lời giải chi tiết câu a, b, c bài 7 như sau:

Câu a:

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

Tập xác định: D = R\{2}.

Giới hạn:

\(\lim_{x\rightarrow +\infty }y= \lim_{x\rightarrow +\infty }\frac{2}{2-x}=0; \lim_{x\rightarrow - \infty }y= \lim_{x\rightarrow -\infty }\frac{2}{2-x}=0\)

\(\lim_{x\rightarrow 2^- }y= \lim_{x\rightarrow 2^- }\frac{2}{2-x}=-\infty; \lim_{x\rightarrow 2^+ }y= \lim_{x\rightarrow 2^+ }\frac{2}{2-x}=+\infty\)

Đồ thị hàm số nhận đường thẳng x = 2 làm tiệm cận đứng và đường thẳng y = 0 làm tiệm cận ngang.

Sự biến thiên: \(y' = \frac{2}{{{{(2 - x)}^2}}} > 0,\forall x \ne 2.\)

Bảng biến thiên:

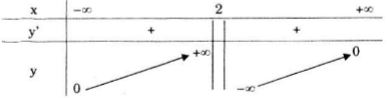
Hàm số đồng biến trên các khoảng \((-\infty ;2)\) và \((2;+\infty )\)

Hàm số không có cực trị:

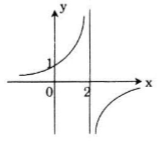
Đồ thị có dạng:

Đồ thị hàm số nhận điểm (2;0) làm tâm đối xứng.

Đồ thị hàm số cắt trục Oy tại điểm (0;1).

Đồ thị hàm số đi qua điểm (1;2).

Câu b:

Hoành độ giao điểm của (C) với đồ thị hàm số y = x² + 1 là nghiệm của phương trình:

\(\frac{2}{2-x}=x^2+1\Leftrightarrow 2=(x^2+1)(2-x)\) với \(x\neq 2\)

\(\Leftrightarrow x(-x^2+2x-1)=0\Leftrightarrow \bigg \lbrack \begin{matrix} x=0\\ x=1 \end{matrix}\)

Ta có \(f'(x)=\frac{2}{(2-x)^2}\)

• Với x = 0 ⇒ y = 1 và \(f'(0)=\frac{1}{2}\)

⇒ phương trình tiếp tuyến có dạng \(y=\frac{1}{2}x+1\).

• Với x = 1 ⇒ y = 2 và f'(1) = 2

⇒ phương trình tiếp tuyến có dạng y = 2(x-1) + 2 hay y = 2x.

Câu c:

Thể tích vật thể tròn xoay cần tìm là:

\(V=\pi \int_{0}^{1}\left ( \frac{2}{2-x} \right )^2dx=4\pi \int_{0}^{1} \frac{dx}{(2-x)^2}=4\pi \frac{1}{2-x} \Bigg |^1_0\)

\(= 4\pi \left ( 1-\frac{1}{2} \right )=2 \pi\) (đvdt).

-- Mod Toán 12