Bài tập 5 trang 146 SGK Giải tích 12

Bài tập 5 trang 146 SGK Giải tích 12

Phương pháp:

Câu a: Sử dụng điều kiện cần để hàm số có cực trị:

Hàm số\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).

Câu b: Áp dụng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn trùng phương.

Câu c: Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại tiếp điểm M(x0,y0) thuộc đồ thị hàm số đã học ở chương trình lớp 11 có dạng:

\(y-y_0=f'(x_0)(x-x_0)\)

Lời giải:

Câu a:

Ta có \(y'=4x^3+2ax\)

Hàm số có cực trị bằng \(\frac{3}{2}\) khi x = 1

\(\Leftrightarrow \left\{\begin{matrix} y'(1)=0\\ y(1)=\frac{3}{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4+2a=0\\ a+b=\frac{1}{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-2\\ b=\frac{5}{2} \end{matrix}\right.\)

Câu b:

Khi \(a=-\frac{1}{2}, b=1\) ta có \(y=x^4-\frac{1}{2}x^2+1\)

Tập xác định: D = R.

Giới hạn: \(\lim_{x\rightarrow \pm \infty }y=+\infty\)

Sự biến thiên:

\(y'=4x^3-x=x(4x^2-1)\)

\(y'=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=0 \ \ (y=1)\\ \\ x=\pm \frac{1}{2} \ \ (y=\frac{15}{16}) \end{matrix}\)

Bảng biến thiên:

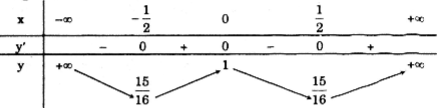
Hàm số đồng biến trên các khoảng \(\left ( -\frac{1}{2};0 \right )\) và \(\left( {\frac{1}{2}; + \infty } \right)\); nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { 0; \frac{1}{2}} \right).\)

Cực trị: 

Hàm số đạt cực đại tại x=0, giá trị cực đại y_cđ=1; Đạt cực tiểu tại \(x=\frac{1}{2}\) và \(x=-\frac{1}{2}\), giá trị cực tiểu \(y_{ct}=\frac{15}{16}.\)

Đồ thị hàm số:

Đồ thị hàm số nhận trục Oy làm trục đối xứng.

Đồ thị hàm số đi qua các điểm \(\left ( 1;\frac{3}{2} \right )\) và \(\left ( -1;\frac{3}{2} \right ).\)

Đồ thị:

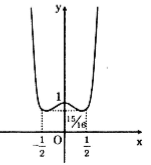
Câu c:

Ta có:

\(y=1\Leftrightarrow x^4-\frac{1}{2}x^2+1=1\Leftrightarrow x^4-\frac{1}{2}x^2=0\)

\(\Leftrightarrow x^2(x^2-\frac{1}{2})=0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=0\\ \\ x=\pm \frac{1}{\sqrt{2}} \end{matrix}\)

Ta có ba tiếp điểm \(A(0;1), B(\frac{1}{\sqrt{2}};1), C(-\frac{1}{\sqrt{2}};1)\)

• Tại A(0;1) ta có y'(0) = 0

Phương trình tiếp tuyến tại A: y - 1 = 0 ⇔ y = 1.

• Tại \(B(\frac{1}{\sqrt{2}};1)\) ta có \(y'(\frac{1}{\sqrt{2}})=\frac{1}{\sqrt{2}}\)

Phương trình tiếp tuyến tại B: \(y-1=\frac{1}{\sqrt{2}}(x-\frac{1}{\sqrt{2}})\Leftrightarrow y= \frac{1}{\sqrt{2}}x+\frac{1}{2}\).

• Tại \(C(-\frac{1}{\sqrt{2}};1)\) ta có \(y'(-\frac{1}{\sqrt{2}})=-\frac{1}{\sqrt{2}}\)

Phương trình tiếp tuyến tại C: \(y-1=-\frac{1}{\sqrt{2}}(x+\frac{1}{\sqrt{2}})\Leftrightarrow y=- \frac{1}{\sqrt{2}}x+\frac{1}{2}\).

-- Mod Toán 12