Bài tập 5.3 trang 219 SBT Toán 12

Bài tập 5.3 trang 219 SBT Toán 12

a) Tập xác định:  D = R\{1}

Đạo hàm: \(y' = \frac{1}{{{{(x - 1)}^2}}}\)

Bảng biến thiên:

 ​

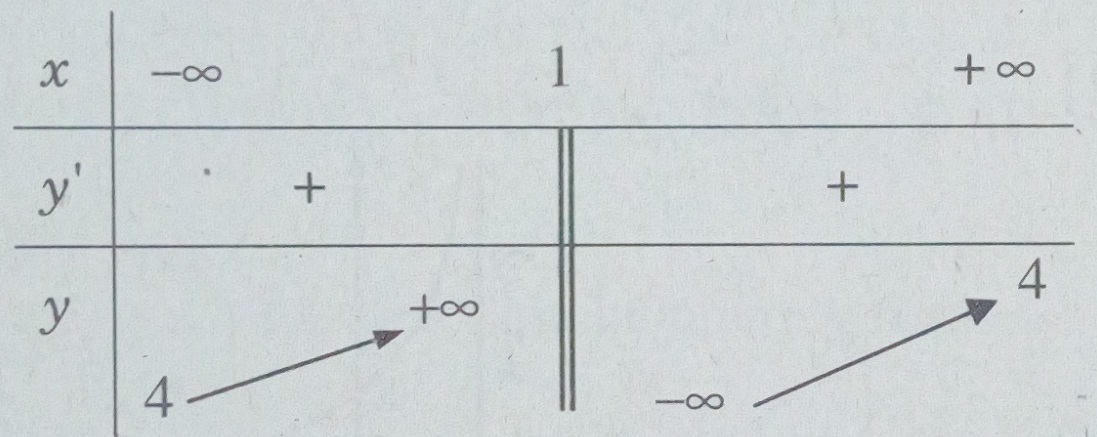
Các khoảng đồng biến là (−∞;1) và (1;+∞)

Tiệm cận đứng x = 1 vì 

\(\mathop {\lim }\limits_{x \to {1^ + }} y =  - \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y =  + \infty \)

Tiệm cận ngang y = 4 vì \(\mathop {\lim }\limits_{x \to  \pm \infty } y = 4\)

Giao với các trục tọa độ: (0; 5) và \(\left( {\frac{5}{4};0} \right)\)

Đồ thị

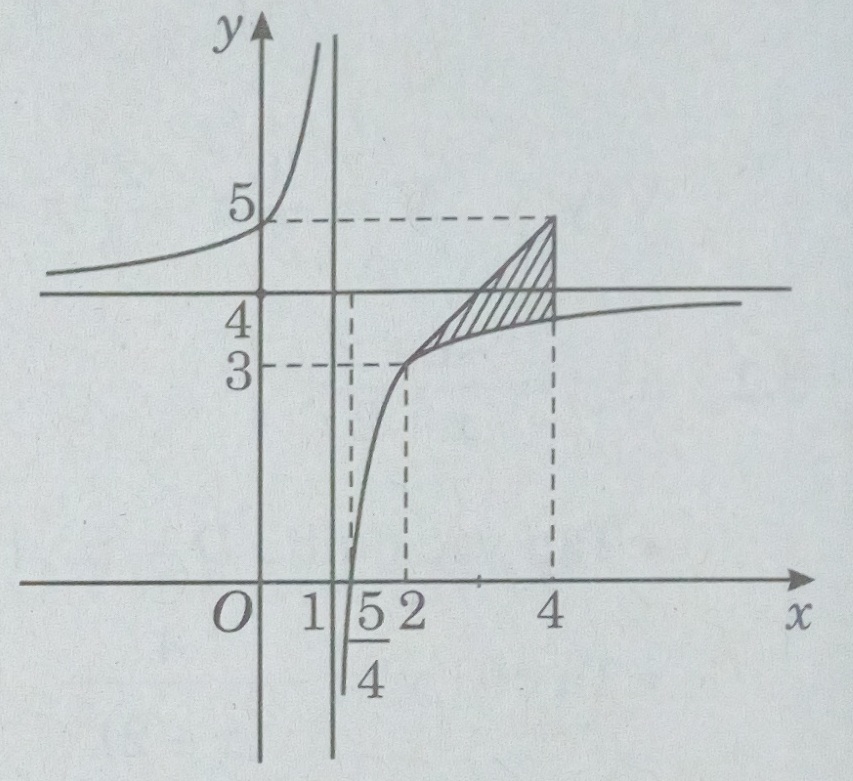
b) Ta có: y’(2) = 1. Phương trình tiếp tuyến là  y = x + 1

Diện tích của miền cần tìm là:

\(\begin{array}{l}
S = \int \limits_2^4 (x + 1 - 4 + \frac{1}{{x - 1}})dx\\
 = \int \limits_2^4 (x - 3 + \frac{1}{{x - 1}})dx = \ln 3
\end{array}\)

-- Mod Toán 12